국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Shortest Paths
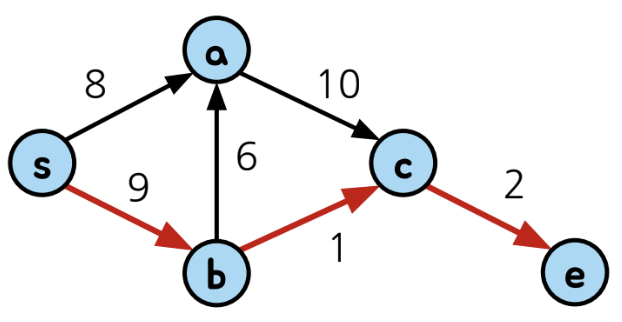
Shortest Paths란 말 그대로 두 점 사이의 최단 경로임
=> 두 점 사이의 경로 중 비용이 최소인 경로
(경로 내 간선들의 비용 합)
Single Source Shortest Paths
그럼 이번 포스팅의 주제인 Single Source Shortest Paths는 뭘까?
이는 한 점과 다른 모든 점 사이의 최단 경로를 의미함
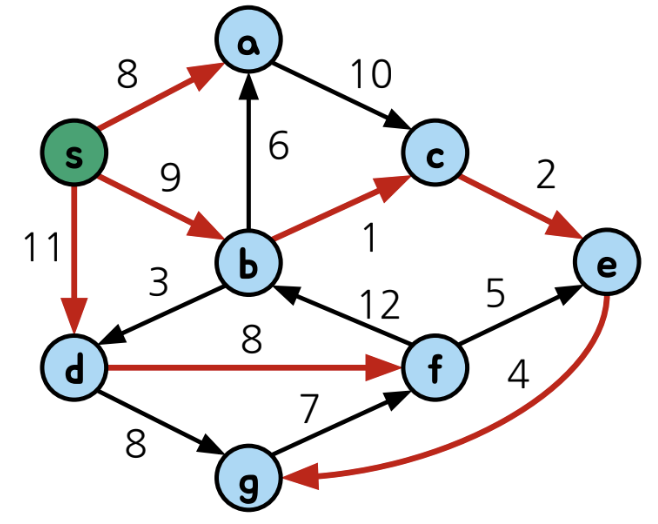
=> 시작 정점 (source node) s에서 다른 모든 점까지의 최단 경로 찾기가 곧, s가 root인 shortest-path tree 찾기임
(일종의 spanning tree라고 볼 수 있음)
Dijkstra's Algorithm
다익스트라 알고리즘은 Single Source Shortest Path를 모두 찾는 알고리즘임
단, 모든 간선의 weight가 0 이상의 값을 가짐
(= 음수 불가)
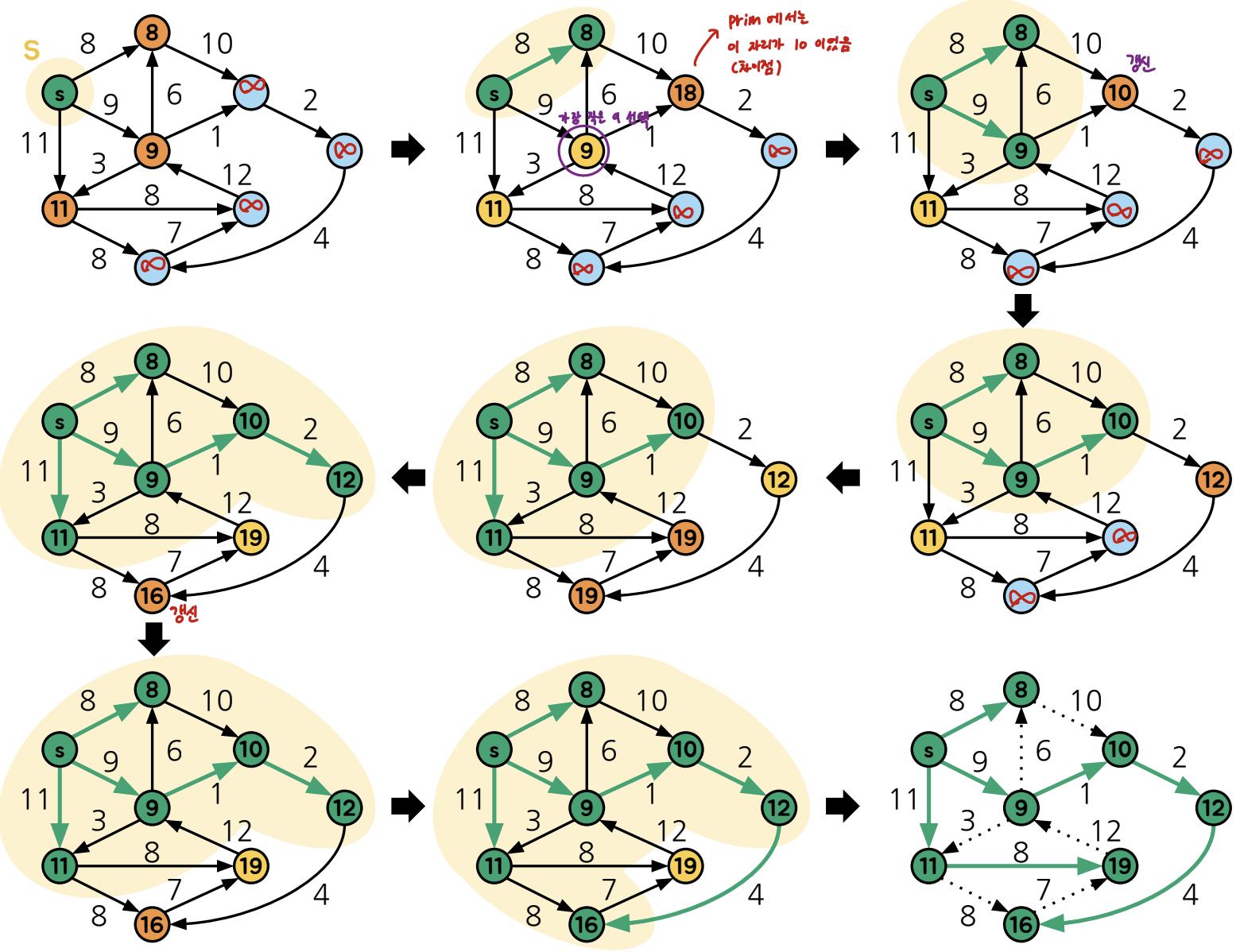
방식은 Prim 알고리즘과 유사한데, 정점 집합 S를 점진적으로 확장해나가는 방식임
1. 시작 정점 s만 포함하는 집합 S={s}를 생성
2. S에 포함되지 않은 정점 중 s와 가장 가까운 정점 v를 찾아 S에 편입
=> v의 이전 노드 저장 (경로 찾을 때 활용)
이제 2번 과정을 모든 정점이 S에 포함될 때 까지 반복하면됨
Prim 알고리즘과의 차이점은
Prim은 집합 S까지의 간선 하나만 확인하는 반면 다익스트라는 시작 정점 s까지의 총 거리로 비교함
pseudo 코드를 살펴보면
# s : 시작 정점, n : 정점 수
prev = [-1] * n # 이전 정점
d = [∞] * n # s와의 거리
d[s] = 0 # 시작 정점인 s를 0으로 하고 나머지를 ∞로 초기화 하면됨
S = set()
Q = min_heap()
Q.enqueue((0, s)) # 순서대로 가중치, node를 의미
while Q is not empty :
w, u = Q.dequeue()
if u in S : continue
S.add(u)
for v, w_uv in neighbors(u) :
if v not in S and d[u] + w_uv < d[v] :
d[v] = d[u] + w_uv
prev[v] = u
Q.enqueue((d[v], v))
다익스트라 알고리즘이 올바르게 최단 경로를 찾는 원리
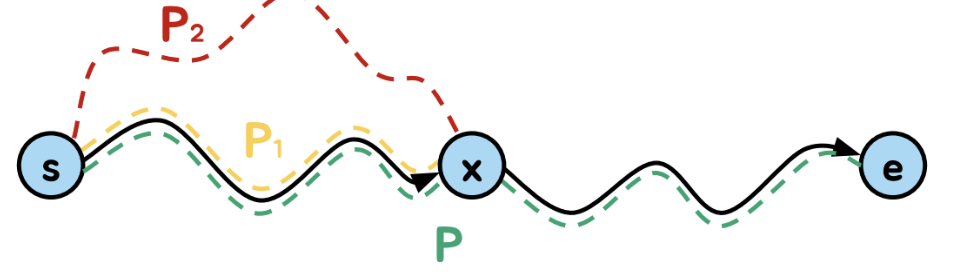
최단 경로의 부분 경로 역시 최단 경로임을 이용함
P가 s와 e 사이의 최단 경로라면,
s와 경로상의 정점 x 사이의 경로 P1도 최단 경로임
=> 만일 s와 x사이에 P1보다 짧은 P2가 존재한다면, s와 e 사이에는 P보다 짧은 경로가 존재하게 되므로 모순!
Discussion
- 시간 복잡도는 Heap에 최대 |E| 개의 값이 들어가고 이를 다시 정점 개수인 |E| 만큼 반복하므로 O(|E|log|E|) 로 볼 수 있지만
|E| < |V|^2 이므로 O(|E|log|E|) = O(2|E|log|V|) = O(|E|log|V|) 로 볼 수 있음 - 다익스트라 알고리즘은 greedy algorithm임
=> 매번 후보 중에서 s와 가장 가까운 정점을 선택하므로 - 다익스트라 알고리즘은 dynamic programming임
=> 거리를 메모리에 저장하여 관리하고, 기존 거리를 활용하여 새로운 거리를 계산하므로
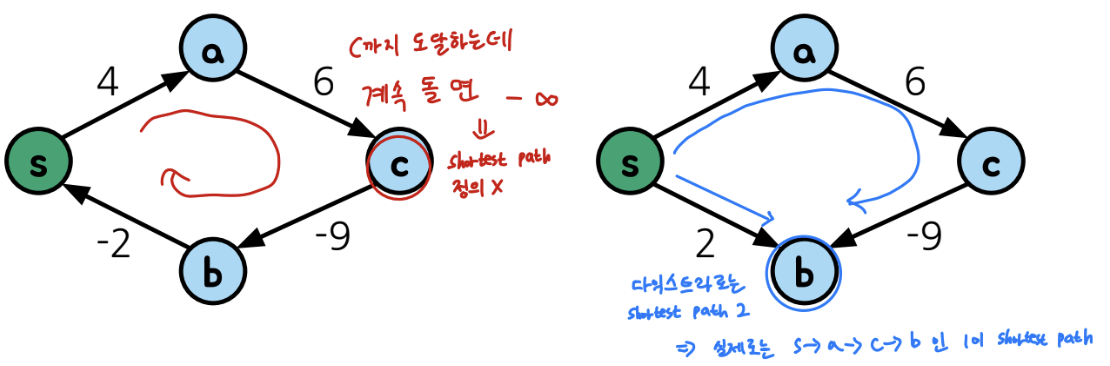
- 다익스트라 알고리즘은 간선의 가중치에 음수가 포함될 경우 잘못 동작함
그림처럼 음의 가중치가 있는 2가지 경우가 있는데
- 음의 사이클이 존재하는 경우 최단경로가 정의되지 않고
- 음의 사이클이 존재하지 않지만 음의 가중치를 갖는 간선이 존재하면 최단경로가 있지만 다익스트라 알고리즘이 답을 못찾음
- 음의 사이클이 존재하는 경우 최단경로가 정의되지 않고
Bellman-Ford Algorithm
벨만-포드 알고리즘은 Single Source Shortest Path들을 찾는 알고리즘임
다익스트라와 다르게 음의 가중치를 허용함
(음의 사이클이 있는 경우는 오류를 반환)
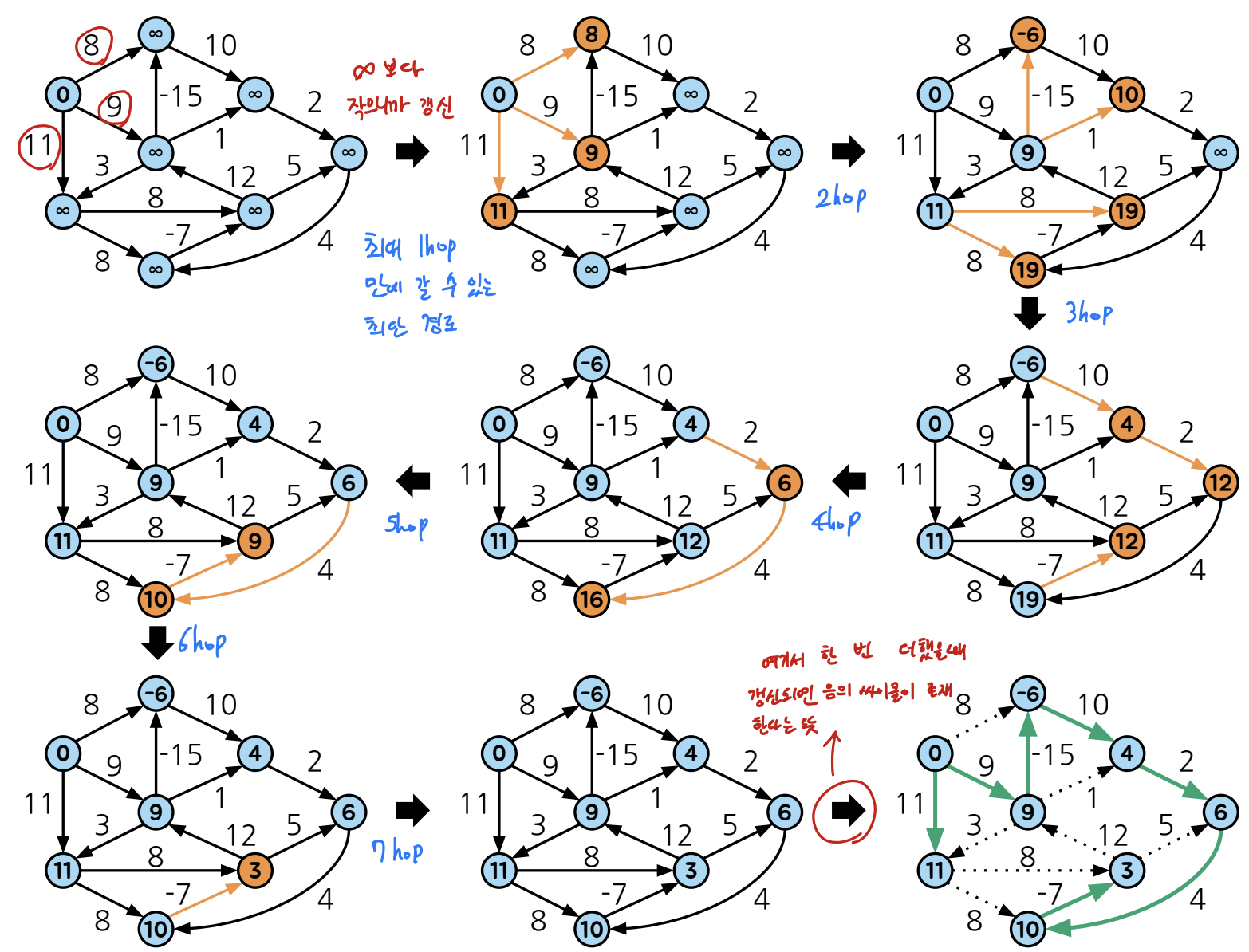
방식은 모든 간선을 반복적으로 탐색하여 시작 정점에서 각 정점까지의 최단거리를 갱신해 나가는 알고리즘임
1. 시작 정점 s의 최단거리 d[s]를 0으로, 나머지 정점 v의 최단거리 d[v]를 무한대로 초기화
2. 모든 간선 (u, v, w_uv)에 대해 d[v]와 경로를 갱신
=> 여기서 d[v] = min(d[v], d[u] + w_uv)
위 2번 과정을 |V| - 1회 반복하면되는데
반복이 끝나고 마지막 과정으로 음의 사이클이 있는지를 확인해야함
이는 d[v] < d[u] + w_uv 인 간선 (u, v, w_uv)가 존재하면 음의 사이클이 존재하는 것으로 판단할 수 있음
(위 그림을 참고하면 이해가 쉬움)
Discussion
pseudo 코드를 살펴보면
# s : 시작정점, n : 정점 수, E : 간선 집합
prev = [-1] * n # 이전 정점 (parent pointer tree)
d = [∞] * n # s와의 거리
d[s] = 0
for _ in range(n - 1) :
for (u, v, w_uv) in E :
if d[u] + w_uv < d[v] :
d[v] = d[u] + w_uv # dp임을 알 수 있음
prev[v] = u
for (u, v, w_uv) in E :
if d[u] + w_uv < d[v] :
#음의 사이클이 존재한다는 뜻
시간 복잡도는 for문을 보면 직관적으로 알 수 있는데, O(|E| * (|V| - 1)) = O(|V||E|) 임
|V| - 1 번 반복하는 이유
경로에 포함된 간선 수는 최대 |V| - 1개 이므로!
(|V| - 1개 보다 많으면 사이클이 존재한다는 뜻임)
음의 사이클이 존재하는 경우
|V| - 1 회 이후에도 더 짧아지는 경로가 발생한다면 그건 음의 사이클이 존재한다는 뜻이 됨
Correctness Analysis
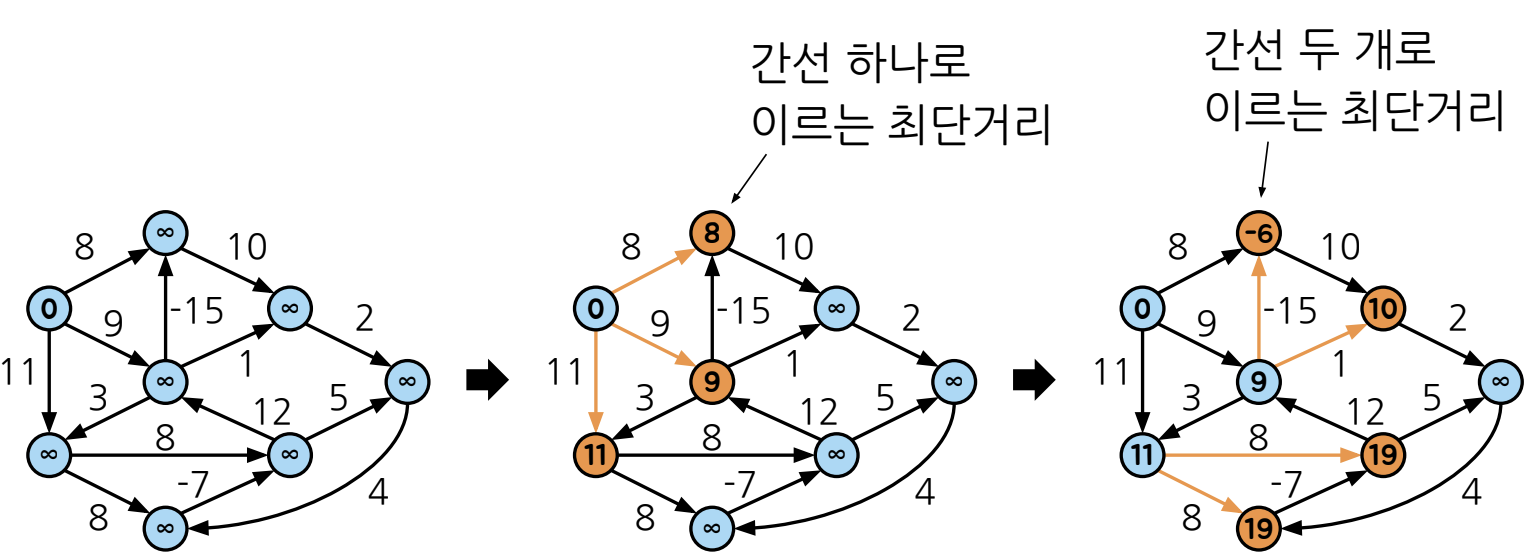
m번 반복 후에는 최대 m개의 간선을 사용해서 얻을 수 있는 최단 경로가 계산됨
=> 최단경로의 최대 길이는 |V| - 1 이므로 |V| - 1회 반복연산 후에는 모든 정점에 이르는 최단 경로가 계산됨
'🔥 Algorithm' 카테고리의 다른 글
| L14 - KMP Algorithm (1) | 2024.11.30 |
|---|---|
| L13 - Topological Sorting (0) | 2024.11.29 |
| L11 - Minimum Spanning Trees (0) | 2024.11.26 |
| L10 - Disjoint Sets (0) | 2024.11.22 |
| L09 - Greedy Algorithms (1) | 2024.11.03 |
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Shortest Paths

Shortest Paths란 말 그대로 두 점 사이의 최단 경로임
=> 두 점 사이의 경로 중 비용이 최소인 경로
(경로 내 간선들의 비용 합)
Single Source Shortest Paths
그럼 이번 포스팅의 주제인 Single Source Shortest Paths는 뭘까?
이는 한 점과 다른 모든 점 사이의 최단 경로를 의미함

=> 시작 정점 (source node) s에서 다른 모든 점까지의 최단 경로 찾기가 곧, s가 root인 shortest-path tree 찾기임
(일종의 spanning tree라고 볼 수 있음)
Dijkstra's Algorithm
다익스트라 알고리즘은 Single Source Shortest Path를 모두 찾는 알고리즘임
단, 모든 간선의 weight가 0 이상의 값을 가짐
(= 음수 불가)

방식은 Prim 알고리즘과 유사한데, 정점 집합 S를 점진적으로 확장해나가는 방식임
1. 시작 정점 s만 포함하는 집합 S={s}를 생성
2. S에 포함되지 않은 정점 중 s와 가장 가까운 정점 v를 찾아 S에 편입
=> v의 이전 노드 저장 (경로 찾을 때 활용)
이제 2번 과정을 모든 정점이 S에 포함될 때 까지 반복하면됨
Prim 알고리즘과의 차이점은
Prim은 집합 S까지의 간선 하나만 확인하는 반면 다익스트라는 시작 정점 s까지의 총 거리로 비교함
pseudo 코드를 살펴보면
# s : 시작 정점, n : 정점 수
prev = [-1] * n # 이전 정점
d = [∞] * n # s와의 거리
d[s] = 0 # 시작 정점인 s를 0으로 하고 나머지를 ∞로 초기화 하면됨
S = set()
Q = min_heap()
Q.enqueue((0, s)) # 순서대로 가중치, node를 의미
while Q is not empty :
w, u = Q.dequeue()
if u in S : continue
S.add(u)
for v, w_uv in neighbors(u) :
if v not in S and d[u] + w_uv < d[v] :
d[v] = d[u] + w_uv
prev[v] = u
Q.enqueue((d[v], v))
다익스트라 알고리즘이 올바르게 최단 경로를 찾는 원리

최단 경로의 부분 경로 역시 최단 경로임을 이용함
P가 s와 e 사이의 최단 경로라면,
s와 경로상의 정점 x 사이의 경로 P1도 최단 경로임
=> 만일 s와 x사이에 P1보다 짧은 P2가 존재한다면, s와 e 사이에는 P보다 짧은 경로가 존재하게 되므로 모순!
Discussion
- 시간 복잡도는 Heap에 최대 |E| 개의 값이 들어가고 이를 다시 정점 개수인 |E| 만큼 반복하므로 O(|E|log|E|) 로 볼 수 있지만
|E| < |V|^2 이므로 O(|E|log|E|) = O(2|E|log|V|) = O(|E|log|V|) 로 볼 수 있음 - 다익스트라 알고리즘은 greedy algorithm임
=> 매번 후보 중에서 s와 가장 가까운 정점을 선택하므로 - 다익스트라 알고리즘은 dynamic programming임
=> 거리를 메모리에 저장하여 관리하고, 기존 거리를 활용하여 새로운 거리를 계산하므로

- 다익스트라 알고리즘은 간선의 가중치에 음수가 포함될 경우 잘못 동작함
그림처럼 음의 가중치가 있는 2가지 경우가 있는데
- 음의 사이클이 존재하는 경우 최단경로가 정의되지 않고
- 음의 사이클이 존재하지 않지만 음의 가중치를 갖는 간선이 존재하면 최단경로가 있지만 다익스트라 알고리즘이 답을 못찾음
- 음의 사이클이 존재하는 경우 최단경로가 정의되지 않고
Bellman-Ford Algorithm
벨만-포드 알고리즘은 Single Source Shortest Path들을 찾는 알고리즘임
다익스트라와 다르게 음의 가중치를 허용함
(음의 사이클이 있는 경우는 오류를 반환)

방식은 모든 간선을 반복적으로 탐색하여 시작 정점에서 각 정점까지의 최단거리를 갱신해 나가는 알고리즘임
1. 시작 정점 s의 최단거리 d[s]를 0으로, 나머지 정점 v의 최단거리 d[v]를 무한대로 초기화
2. 모든 간선 (u, v, w_uv)에 대해 d[v]와 경로를 갱신
=> 여기서 d[v] = min(d[v], d[u] + w_uv)
위 2번 과정을 |V| - 1회 반복하면되는데
반복이 끝나고 마지막 과정으로 음의 사이클이 있는지를 확인해야함
이는 d[v] < d[u] + w_uv 인 간선 (u, v, w_uv)가 존재하면 음의 사이클이 존재하는 것으로 판단할 수 있음
(위 그림을 참고하면 이해가 쉬움)
Discussion
pseudo 코드를 살펴보면
# s : 시작정점, n : 정점 수, E : 간선 집합
prev = [-1] * n # 이전 정점 (parent pointer tree)
d = [∞] * n # s와의 거리
d[s] = 0
for _ in range(n - 1) :
for (u, v, w_uv) in E :
if d[u] + w_uv < d[v] :
d[v] = d[u] + w_uv # dp임을 알 수 있음
prev[v] = u
for (u, v, w_uv) in E :
if d[u] + w_uv < d[v] :
#음의 사이클이 존재한다는 뜻
시간 복잡도는 for문을 보면 직관적으로 알 수 있는데, O(|E| * (|V| - 1)) = O(|V||E|) 임
|V| - 1 번 반복하는 이유
경로에 포함된 간선 수는 최대 |V| - 1개 이므로!
(|V| - 1개 보다 많으면 사이클이 존재한다는 뜻임)
음의 사이클이 존재하는 경우
|V| - 1 회 이후에도 더 짧아지는 경로가 발생한다면 그건 음의 사이클이 존재한다는 뜻이 됨
Correctness Analysis

m번 반복 후에는 최대 m개의 간선을 사용해서 얻을 수 있는 최단 경로가 계산됨
=> 최단경로의 최대 길이는 |V| - 1 이므로 |V| - 1회 반복연산 후에는 모든 정점에 이르는 최단 경로가 계산됨
'🔥 Algorithm' 카테고리의 다른 글
| L14 - KMP Algorithm (1) | 2024.11.30 |
|---|---|
| L13 - Topological Sorting (0) | 2024.11.29 |
| L11 - Minimum Spanning Trees (0) | 2024.11.26 |
| L10 - Disjoint Sets (0) | 2024.11.22 |
| L09 - Greedy Algorithms (1) | 2024.11.03 |
