국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Minimum Spanning Trees

Spanning Tree란 그래프 G = (V, E)에서 간선을 |V| - 1 개만 남겨 트리가 되도록 만든 것
Minimm Spanning Tree란 Spanning Tree 중에서 edge weight의 합이 가장 작은 것
=> 한 그래프에 여러개의 MST가 존재할 수 있음
어떻게 MST를 구할까..?
Naive Solution을 생각해보면
모든 subgraph를 살펴보고, 그 중에서 spanning tree이면서 weight의 합이 가장 작은 것을 찾으면됨
=> subgraph의 수는 각각의 edge가 있냐 없냐에 따라 결정되므로 2^|E| 임
(큰 그래프는 사실상 처리 불가)
이에 대해 효율적인 크루스칼, 프림 알고리즘이 존재함
(둘다 Greedy Algorithm)
Kruskal's Algorithm
Cycle을 만들지 않는 최소 간선을 MST에 반복하여 추가하는 것임
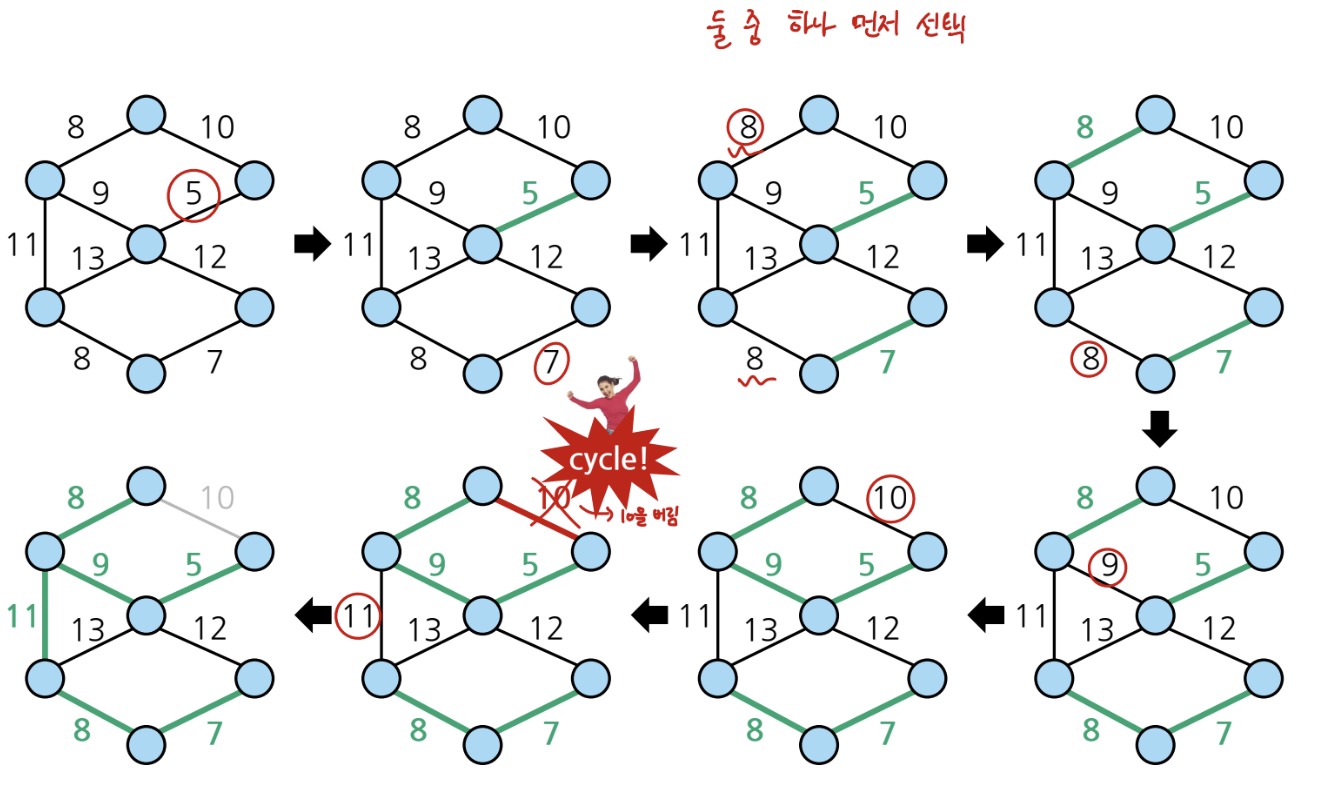
순서는
1. 간선을 weight를 기준으로 오름차순 정렬
2. weight가 가장 작은 간선을 선택하고 이미 MST에 추가된 간선들과 cycle을 이루는지 확인
=> cycle을 이루는 경우 간선을 제외하고 이루지 않는 경우 간선을 MST에 추가
3. |V| - 1 개의 간선이 선택될 때 까지 Step 2를 반복
Cycle을 효율적으로 확인하기 위해 Disjoint Set을 활용
Disjoint Set이 기억이 안나면
https://hanjungyo.tistory.com/96
L10 - Disjoint Sets
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한 박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다 Disjoint Sets Disjoint Sets란 서로 겹치지 않는 집합들을 의미함 =>
hanjungyo.tistory.com
그래서 결론적으로 Disjoint Set을 활용해 Cycle을 확인하는 방법은

- 각 정점이 독립된 집합을 이루도록 초기화 (make-set)
- 간선 (u, v)가 MST에 추가될 때 union(u, v) 실행
- 간선 (u, v)가 cycle을 이룬다는건 u와 v가 같은 집합에 있다는 뜻
=> 즉, find-set(u) = find-set(v)인 경우 cycle을 이룸
Complexity Analysis
pseudo code를 살펴보면
mst = [] # edges of MST
for u in range(n + 1) :
make_set(u)
#sort by weight
edges.sort(lambda x: x[2])
for u, v in edges :
if find_set(u) != find_set(v) :
mst.append((u, v))
union(u, v)
Space Complexity
- Edges : O(|E|)
=> edge만 입력으로 주면 되므로
(edge만 정렬, 순회함) - Disjoint sets : O(|V|)
=> 각 노드가 부모 정보를 가지므로 노드의 개수와 동일 - Total : O(|V| + |E|)
Time Complexity
- Sorting : O(|E|log|E|)
=> 여기서 E는 최대 V^2 이므로 |E|log|V|^2 = 2|E|log|V| = O(|E|log|V|)로 볼 수 있음 - Disjoint sets : O(|E|log*|V|)
=> log*은 사실상 상수이므로 Sorting이 우세항으로 작용 - Total : O(|E|log|V|)
Prim's Algorithm
MST에 가장 가까운 정점을 반복하여 추가하는 것임

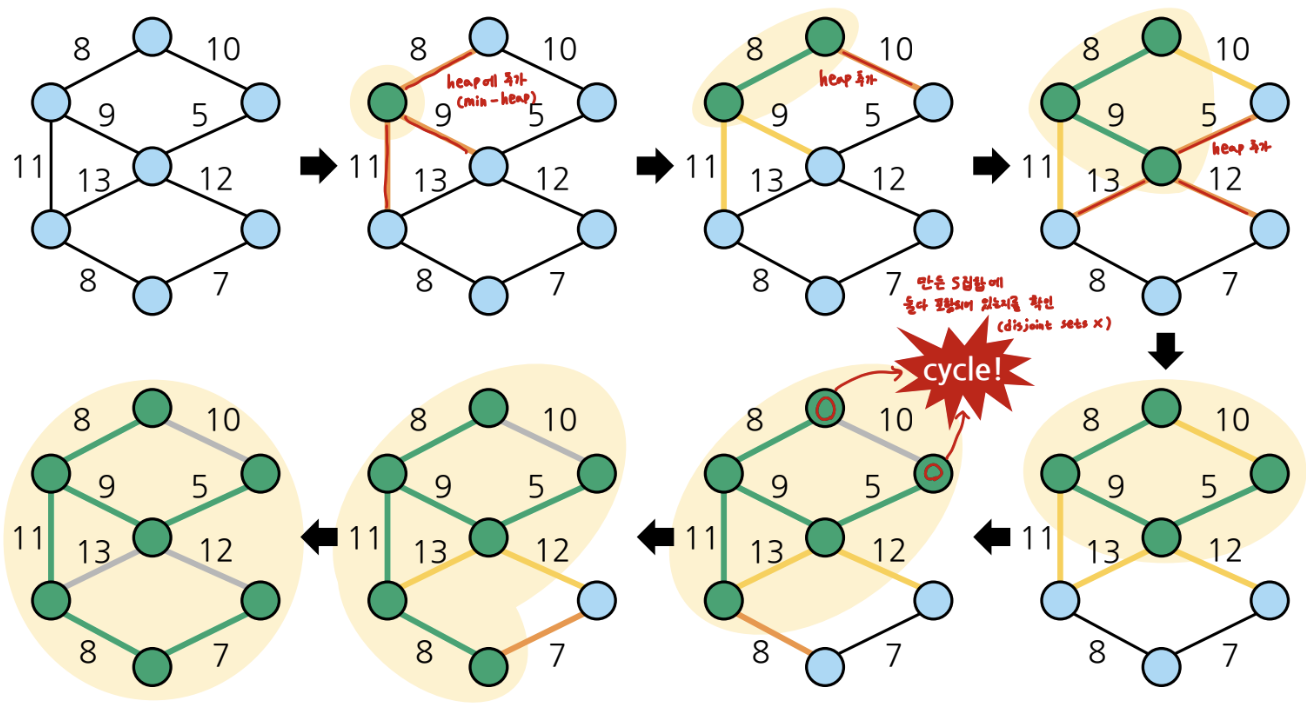
순서는
1. 아무 정점 하나를 선택하여 MST에 추가
2. MST와 직접 연결된 외부의 정점 중 가장 가까운 정점을 MST에 추가
3. 모든 정점이 MST에 추가될 때 까지 반복
어떻게 후보 간선들 중 가장 짧은 애를 찾을 수 있을까?
min-heap을 활용하면 됨
pseudo code를 살펴보면
mst = []
Q = min_heap()
Q.enqueue((0, 0, None)) # 순서대로 weight, node, MST안의 나와 연결된 node
S = {}
while Q is not empty :
w, u, p = Q.dequeue()
if u in S : continue # 이미 MST에 들어갔다는 뜻
S.add(u)
mst.append((p, u))
for v, w_uv in neighbors(u) :
if v not in S :
Q.enqueue((w_uv, v, u))
Complexity Analysis
Space Complexity
- 인접리스트 그래프 : O(|E| + |V|)
=> neighbors에서 인접 리스트를 쓰는게 효율적이기 때문에 인접 리스트 사용 - min-heap : O(|E|)
=> 간선들을 다 넣으므로 - S : O(|V|)
=> 최대 크기가 정점의 개수이므로 - Total : O(|V| + |E|)
Time Complexity
- min-heap : O(|E|log|E|)
=> 위에서 다룬 내용과 동일하게 O(|E|log|V|)로 볼 수 있음
(min-heap에 간선 넣을 때 최대 log|E|를 edge수인 |E| 만큼 반복)
Correctness Analysis
Kruskal's, Prim's Algorithm의 정당성?

전체 정점 집합 V를 S, V - S로 나눴을 때 S와 V - S 사이를 연결하는 가장 짧은 간선을 e라 하면, e를 포함하는 MST가 반드시 존재함
e를 포함하지 않는 MST인 T가 존재한다고 가정해보자
e = (u, v) 일 때, MST에서 u와 v사이의 경로 P는 유일함
=> P에서 S와 V - S 사이를 지나는 간선 e'은 유일
(2개 있으면 cycle)
e'을 지우고 e를 추가한 T'는 또다른 Spanning Tree인데
1. w(e') > w(e) 인 경우 T는 MST가 아님 (모순)
2. w(e') = w(e) 인 경우 T'는 e를 포함한 MST
'🔥 Algorithm' 카테고리의 다른 글
| L13 - Topological Sorting (0) | 2024.11.29 |
|---|---|
| L12 - Single Source Shortest Paths (0) | 2024.11.28 |
| L10 - Disjoint Sets (0) | 2024.11.22 |
| L09 - Greedy Algorithms (1) | 2024.11.03 |
| L07 - Selection (4) | 2024.10.13 |
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Minimum Spanning Trees

Spanning Tree란 그래프 G = (V, E)에서 간선을 |V| - 1 개만 남겨 트리가 되도록 만든 것
Minimm Spanning Tree란 Spanning Tree 중에서 edge weight의 합이 가장 작은 것
=> 한 그래프에 여러개의 MST가 존재할 수 있음
어떻게 MST를 구할까..?
Naive Solution을 생각해보면
모든 subgraph를 살펴보고, 그 중에서 spanning tree이면서 weight의 합이 가장 작은 것을 찾으면됨
=> subgraph의 수는 각각의 edge가 있냐 없냐에 따라 결정되므로 2^|E| 임
(큰 그래프는 사실상 처리 불가)
이에 대해 효율적인 크루스칼, 프림 알고리즘이 존재함
(둘다 Greedy Algorithm)
Kruskal's Algorithm
Cycle을 만들지 않는 최소 간선을 MST에 반복하여 추가하는 것임

순서는
1. 간선을 weight를 기준으로 오름차순 정렬
2. weight가 가장 작은 간선을 선택하고 이미 MST에 추가된 간선들과 cycle을 이루는지 확인
=> cycle을 이루는 경우 간선을 제외하고 이루지 않는 경우 간선을 MST에 추가
3. |V| - 1 개의 간선이 선택될 때 까지 Step 2를 반복
Cycle을 효율적으로 확인하기 위해 Disjoint Set을 활용
Disjoint Set이 기억이 안나면
https://hanjungyo.tistory.com/96
L10 - Disjoint Sets
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한 박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다 Disjoint Sets Disjoint Sets란 서로 겹치지 않는 집합들을 의미함 =>
hanjungyo.tistory.com
그래서 결론적으로 Disjoint Set을 활용해 Cycle을 확인하는 방법은

- 각 정점이 독립된 집합을 이루도록 초기화 (make-set)
- 간선 (u, v)가 MST에 추가될 때 union(u, v) 실행
- 간선 (u, v)가 cycle을 이룬다는건 u와 v가 같은 집합에 있다는 뜻
=> 즉, find-set(u) = find-set(v)인 경우 cycle을 이룸
Complexity Analysis
pseudo code를 살펴보면
mst = [] # edges of MST
for u in range(n + 1) :
make_set(u)
#sort by weight
edges.sort(lambda x: x[2])
for u, v in edges :
if find_set(u) != find_set(v) :
mst.append((u, v))
union(u, v)
Space Complexity
- Edges : O(|E|)
=> edge만 입력으로 주면 되므로
(edge만 정렬, 순회함) - Disjoint sets : O(|V|)
=> 각 노드가 부모 정보를 가지므로 노드의 개수와 동일 - Total : O(|V| + |E|)
Time Complexity
- Sorting : O(|E|log|E|)
=> 여기서 E는 최대 V^2 이므로 |E|log|V|^2 = 2|E|log|V| = O(|E|log|V|)로 볼 수 있음 - Disjoint sets : O(|E|log*|V|)
=> log*은 사실상 상수이므로 Sorting이 우세항으로 작용 - Total : O(|E|log|V|)
Prim's Algorithm
MST에 가장 가까운 정점을 반복하여 추가하는 것임


순서는
1. 아무 정점 하나를 선택하여 MST에 추가
2. MST와 직접 연결된 외부의 정점 중 가장 가까운 정점을 MST에 추가
3. 모든 정점이 MST에 추가될 때 까지 반복
어떻게 후보 간선들 중 가장 짧은 애를 찾을 수 있을까?
min-heap을 활용하면 됨
pseudo code를 살펴보면
mst = []
Q = min_heap()
Q.enqueue((0, 0, None)) # 순서대로 weight, node, MST안의 나와 연결된 node
S = {}
while Q is not empty :
w, u, p = Q.dequeue()
if u in S : continue # 이미 MST에 들어갔다는 뜻
S.add(u)
mst.append((p, u))
for v, w_uv in neighbors(u) :
if v not in S :
Q.enqueue((w_uv, v, u))
Complexity Analysis
Space Complexity
- 인접리스트 그래프 : O(|E| + |V|)
=> neighbors에서 인접 리스트를 쓰는게 효율적이기 때문에 인접 리스트 사용 - min-heap : O(|E|)
=> 간선들을 다 넣으므로 - S : O(|V|)
=> 최대 크기가 정점의 개수이므로 - Total : O(|V| + |E|)
Time Complexity
- min-heap : O(|E|log|E|)
=> 위에서 다룬 내용과 동일하게 O(|E|log|V|)로 볼 수 있음
(min-heap에 간선 넣을 때 최대 log|E|를 edge수인 |E| 만큼 반복)
Correctness Analysis
Kruskal's, Prim's Algorithm의 정당성?

전체 정점 집합 V를 S, V - S로 나눴을 때 S와 V - S 사이를 연결하는 가장 짧은 간선을 e라 하면, e를 포함하는 MST가 반드시 존재함
e를 포함하지 않는 MST인 T가 존재한다고 가정해보자
e = (u, v) 일 때, MST에서 u와 v사이의 경로 P는 유일함
=> P에서 S와 V - S 사이를 지나는 간선 e'은 유일
(2개 있으면 cycle)
e'을 지우고 e를 추가한 T'는 또다른 Spanning Tree인데
1. w(e') > w(e) 인 경우 T는 MST가 아님 (모순)
2. w(e') = w(e) 인 경우 T'는 e를 포함한 MST
'🔥 Algorithm' 카테고리의 다른 글
| L13 - Topological Sorting (0) | 2024.11.29 |
|---|---|
| L12 - Single Source Shortest Paths (0) | 2024.11.28 |
| L10 - Disjoint Sets (0) | 2024.11.22 |
| L09 - Greedy Algorithms (1) | 2024.11.03 |
| L07 - Selection (4) | 2024.10.13 |
