국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Disjoint Sets
Disjoint Sets란 서로 겹치지 않는 집합들을 의미함
=> 어쩌피 교집합이 공집합이므로 intersect 연산은 따로 존재 X
∴ Disjoint Set 연산에는
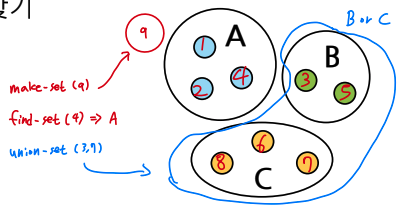
- make-set(u) : u를 유일한 원소로 갖는 집합 생성
- find-set(u) : u가 속한 집합 리턴
- union(u, v) : u가 속한 집합과 v가 속한 집합을 합침
https://www.acmicpc.net/problem/1717
집합의 표현 이라는 백준 문제를 Disjoint Set 연산으로 해결하는 코드를 살펴보자

python의 set을 쓴다면 union(u, v)를 할 때 u, v가 속한 집합을 찾기위해 각각 O(n) 만큼 시간이 걸리고
u, v가 속한 집합을 합치기 위해 한 쪽에 값을 다 넣는데 시간이 또 걸림
=> 한 번에 찾을 수 있게 배열을 만든어놔도 합집합을 할 때 결국 n만큼 걸리므로 비효율적
Naive Implementation of Disjoint Sets
배열을 이용하여 각 원소가 속한 집합을 표현해보는 방법을 생각할 수 있음
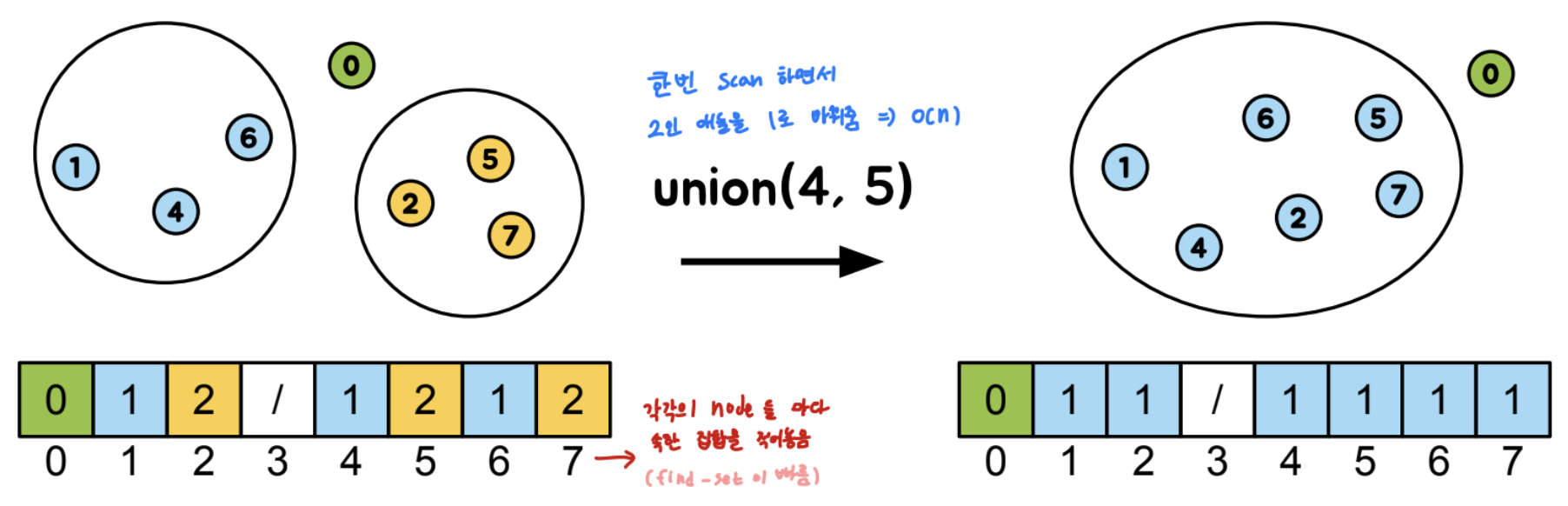
- arr[u]는 u가 속한 집합을 의미
- make-set(u) : arr[u] = u 로 초기화
=> O(1) - find-set(u) : arr[u]를 리턴
=> O(1) - union(u, v) : v가 속한 집합의 값을 u의 집합으로 변경
=> O(n)
(배열을 한번 scan 하면서 속한 집합을 바꿔줘야하므로)
Parent Pointer Trees for Disjoint Sets
각 Tree가 집합을 나타내도록 구현
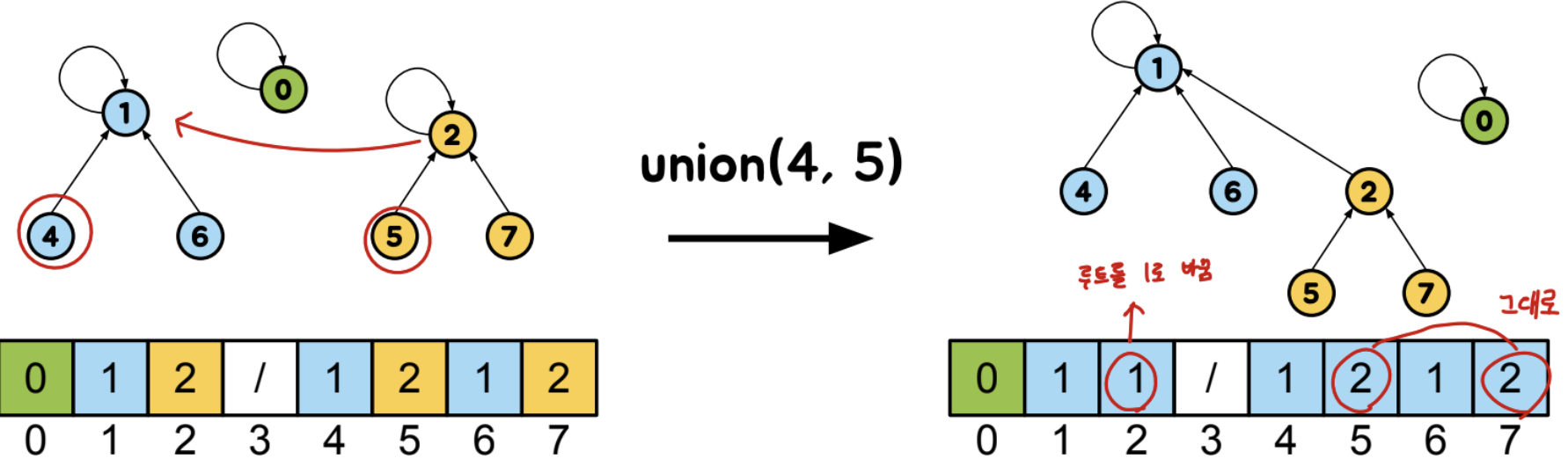
- Tree의 root는 해당 집합의 대표 노드임
- find-set(u) : u가 속한 tree의 root를 리턴
=> O(tree 높이)
(root까지 쭉 올라가서 확인하므로) - union-set(u, v) : v가 속한 tree의 root를 u가 속한 tree의 root에 연결
=> O(tree 높이)
(u, v의 root를 확인하고 둘 중 하나의 root를 변경하므로 O(tree의 높이) + O(tree의 높이) + O(1) = O(tree의 높이) 가 됨)
하지만 각 노드가 하나씩 연결된다면 최악의 경우 tree의 높이는 n이 됨
=> find-set 와 union-set 모두 O(n)이 되버리는 창조 손해가 발생함
그럼 이제 어떻게 tree의 높이를 낮게 유지할 수 있는지를 고민해봐야함
tree의 높이를 낮게 유지할 수 있는 최적화 방법 Union by Rank와 Path Compression을 살펴보자
Union by Rank
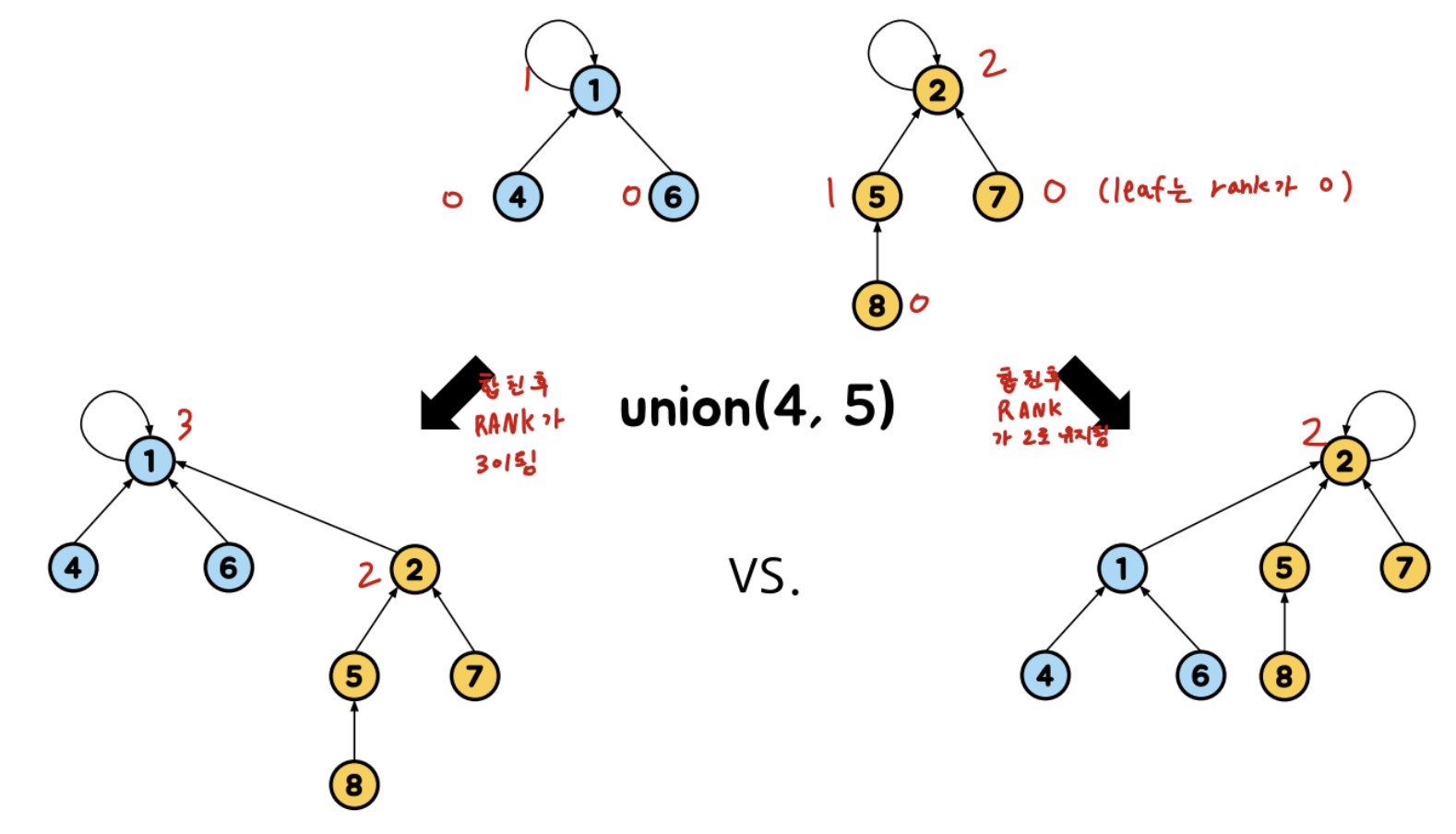
2개의 Tree를 Union할 때, 높이가 낮은 Tree를 높은 Tree에 연결
여기서 생각해야할 부분은 2개의 tree의 rank가 같을 때 높이가 증가한다는 것임
=> 만약 tree A와 B 둘 중 하나가 큰 경우 합치면 더 큰 rank를 따라감
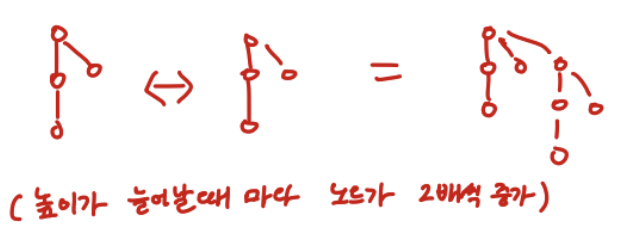
- A의 높이 > B의 높이 => A의 높이
- A의 높이 < B의 높이 => B의 높이
- A의 높이 = B의 높이 => (A 또는 B의 높이) + 1
위 그림에서 하나 더 알 수 있는 사실은 높이가 늘어날 때 마다 노드가 2배씩 증가한다는 것임
즉, 높이가 h인 Tree는 최소 2^h 개의 노드를 가짐 (n >= 2^h)
=> 노드가 n개인 Tree의 높이는 최대 logn (logn >= h)
Tree의 높이를 더 줄이려면..?
Path Compression
Find-set(u) 연산을 수행할 때, 경로상의 모든 노드를 Root에 연결
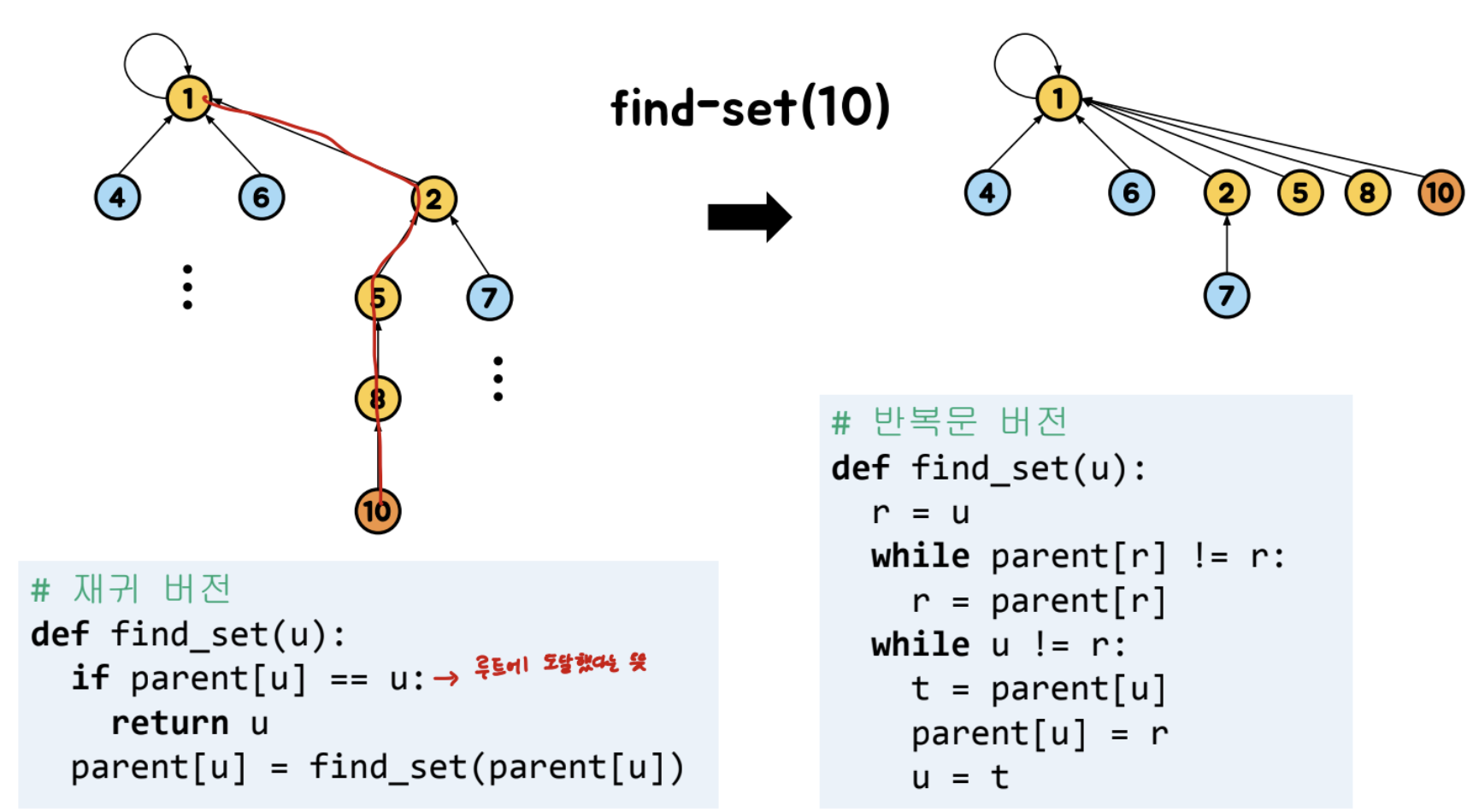
Complexity Analysis
n번의 make-set 연산과 m번의 union/find-set 연산이 수행될 경우 시간복잡도를 살펴보면
- Union by Rank
=> O(mlogn) - Path Compression 적용
=> O(mlog*n)
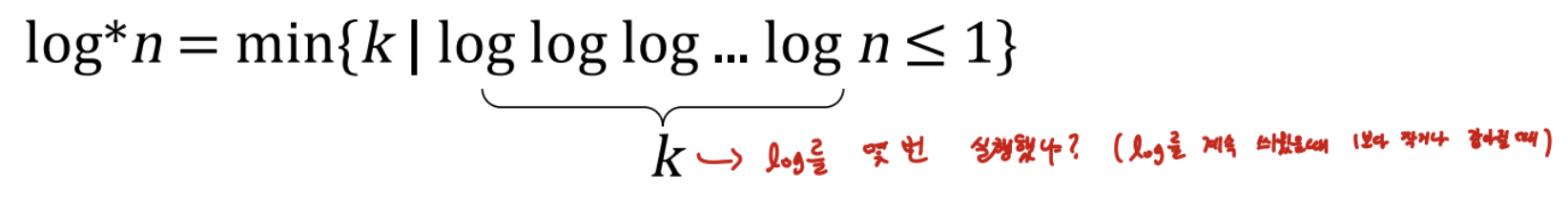
=> log*n은 사실상 상수라고 봐도 될 정도로 작음
따라서 사실상 Path Compression의 시간복잡도는 O(m)임!
Path Compression 할 때 두 번 반복하는 것을 피하려면?
Additional Issues
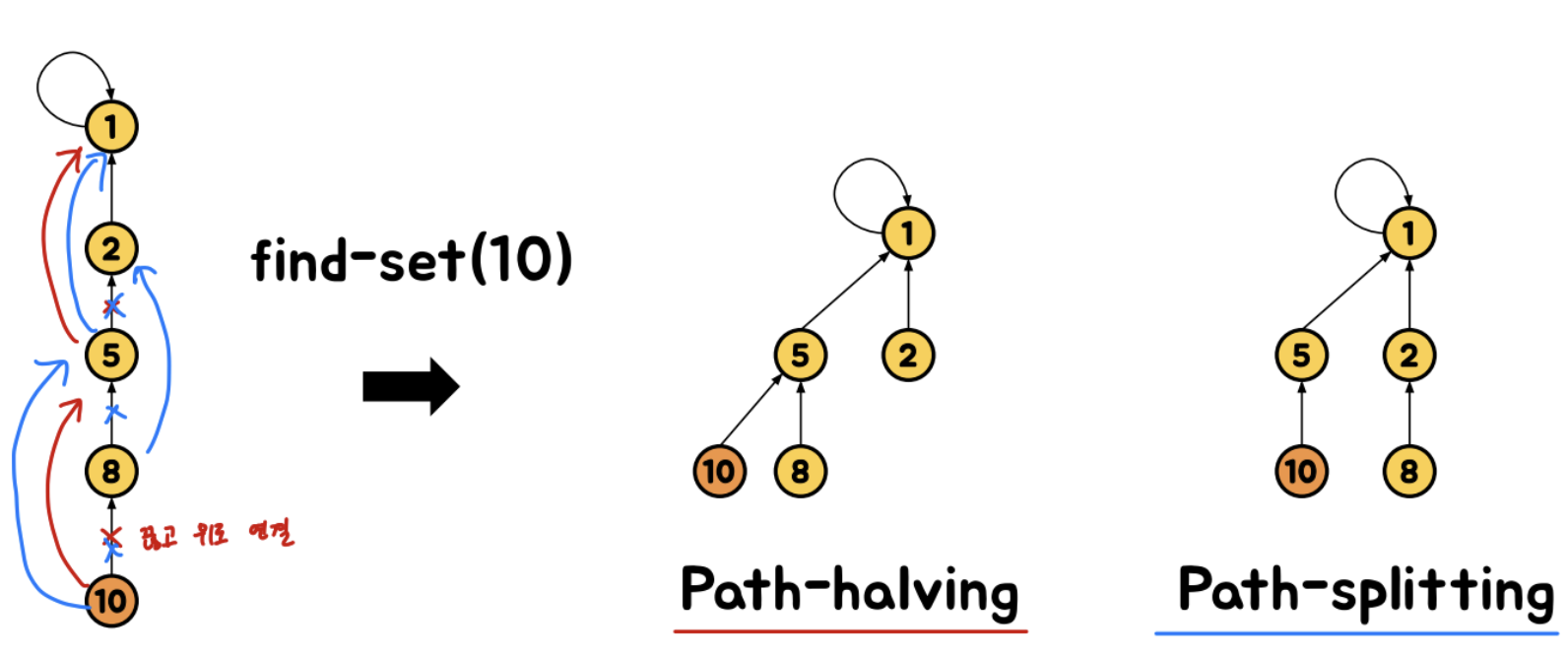
Root로 연결하는 대신에 조부모에 연결
=> 경로의 길이가 절반으로 줄어드는 효과
Path-halving의 경우 : 부모의 연결을 끊고 그 위의 조부모랑 연결함
(이 때 연결이 끊긴 부모는 추가적으로 뭘 하지 않고 넘어감)
Path-splitting의 경우 : 부모의 연결을 끊고 그 위의 조부모랑 연결함
(이 때 연결이 끊긴 부모도 같은 과정을 실행)
공통 조상이 있는 두 노드 u, v에 대해 union 연산을 빨리 끝내려면?
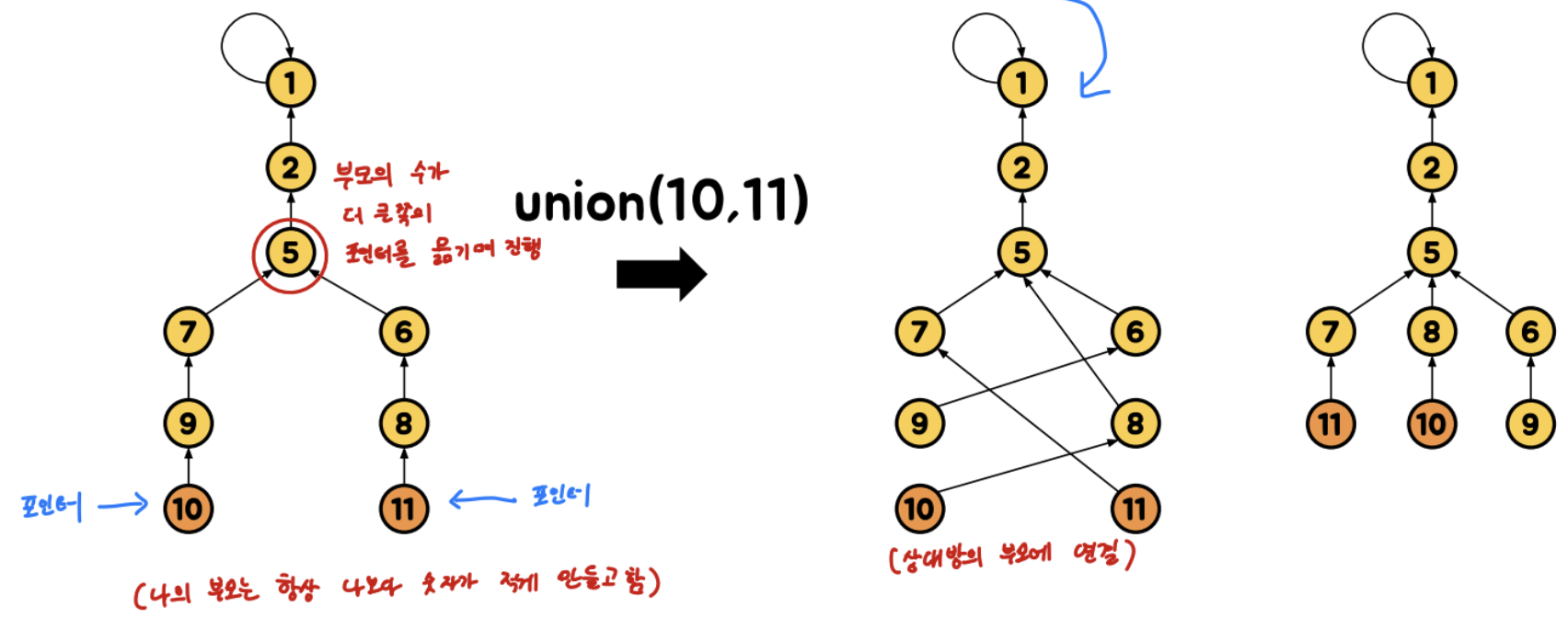
기존 find-set(u), find-set(v) 를 실행하면 Root까지 연산하지만
Rem's Algorithm은 공통 조상이 나타나면 연산 종료
1. 나의 부모가 항상 나보다 숫자가 적은 상태로 만든 후
2. 각 leaf에 포인터를 지정해놓고 시작
3. 부모를 확인하고 부모의 수가 더 큰쪽으로 포인터를 하나 올림
4. 이를 반복하다 양쪽 부모의 수가 같아지는 즉, 공통 조상이 나타나면 연산 종료
이 때 find-set을 쓰지 않으므로 Path Compression이 어렵기 때문에 Splicing 기법 적용
=> 포인터가 위로 올라갈 때 자기 부모와의 연결을 끊고 상대 포인터의 부모랑 연결
'🔥 Algorithm' 카테고리의 다른 글
| L12 - Single Source Shortest Paths (0) | 2024.11.28 |
|---|---|
| L11 - Minimum Spanning Trees (0) | 2024.11.26 |
| L09 - Greedy Algorithms (1) | 2024.11.03 |
| L07 - Selection (4) | 2024.10.13 |
| L06 - Non-comparison Sorting (2) | 2024.10.08 |
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Disjoint Sets
Disjoint Sets란 서로 겹치지 않는 집합들을 의미함
=> 어쩌피 교집합이 공집합이므로 intersect 연산은 따로 존재 X
∴ Disjoint Set 연산에는

- make-set(u) : u를 유일한 원소로 갖는 집합 생성
- find-set(u) : u가 속한 집합 리턴
- union(u, v) : u가 속한 집합과 v가 속한 집합을 합침
https://www.acmicpc.net/problem/1717
집합의 표현 이라는 백준 문제를 Disjoint Set 연산으로 해결하는 코드를 살펴보자

python의 set을 쓴다면 union(u, v)를 할 때 u, v가 속한 집합을 찾기위해 각각 O(n) 만큼 시간이 걸리고
u, v가 속한 집합을 합치기 위해 한 쪽에 값을 다 넣는데 시간이 또 걸림
=> 한 번에 찾을 수 있게 배열을 만든어놔도 합집합을 할 때 결국 n만큼 걸리므로 비효율적
Naive Implementation of Disjoint Sets
배열을 이용하여 각 원소가 속한 집합을 표현해보는 방법을 생각할 수 있음

- arr[u]는 u가 속한 집합을 의미
- make-set(u) : arr[u] = u 로 초기화
=> O(1) - find-set(u) : arr[u]를 리턴
=> O(1) - union(u, v) : v가 속한 집합의 값을 u의 집합으로 변경
=> O(n)
(배열을 한번 scan 하면서 속한 집합을 바꿔줘야하므로)
Parent Pointer Trees for Disjoint Sets
각 Tree가 집합을 나타내도록 구현

- Tree의 root는 해당 집합의 대표 노드임
- find-set(u) : u가 속한 tree의 root를 리턴
=> O(tree 높이)
(root까지 쭉 올라가서 확인하므로) - union-set(u, v) : v가 속한 tree의 root를 u가 속한 tree의 root에 연결
=> O(tree 높이)
(u, v의 root를 확인하고 둘 중 하나의 root를 변경하므로 O(tree의 높이) + O(tree의 높이) + O(1) = O(tree의 높이) 가 됨)
하지만 각 노드가 하나씩 연결된다면 최악의 경우 tree의 높이는 n이 됨
=> find-set 와 union-set 모두 O(n)이 되버리는 창조 손해가 발생함
그럼 이제 어떻게 tree의 높이를 낮게 유지할 수 있는지를 고민해봐야함
tree의 높이를 낮게 유지할 수 있는 최적화 방법 Union by Rank와 Path Compression을 살펴보자
Union by Rank

2개의 Tree를 Union할 때, 높이가 낮은 Tree를 높은 Tree에 연결
여기서 생각해야할 부분은 2개의 tree의 rank가 같을 때 높이가 증가한다는 것임
=> 만약 tree A와 B 둘 중 하나가 큰 경우 합치면 더 큰 rank를 따라감

- A의 높이 > B의 높이 => A의 높이
- A의 높이 < B의 높이 => B의 높이
- A의 높이 = B의 높이 => (A 또는 B의 높이) + 1
위 그림에서 하나 더 알 수 있는 사실은 높이가 늘어날 때 마다 노드가 2배씩 증가한다는 것임
즉, 높이가 h인 Tree는 최소 2^h 개의 노드를 가짐 (n >= 2^h)
=> 노드가 n개인 Tree의 높이는 최대 logn (logn >= h)
Tree의 높이를 더 줄이려면..?
Path Compression
Find-set(u) 연산을 수행할 때, 경로상의 모든 노드를 Root에 연결

Complexity Analysis
n번의 make-set 연산과 m번의 union/find-set 연산이 수행될 경우 시간복잡도를 살펴보면
- Union by Rank
=> O(mlogn) - Path Compression 적용
=> O(mlog*n)
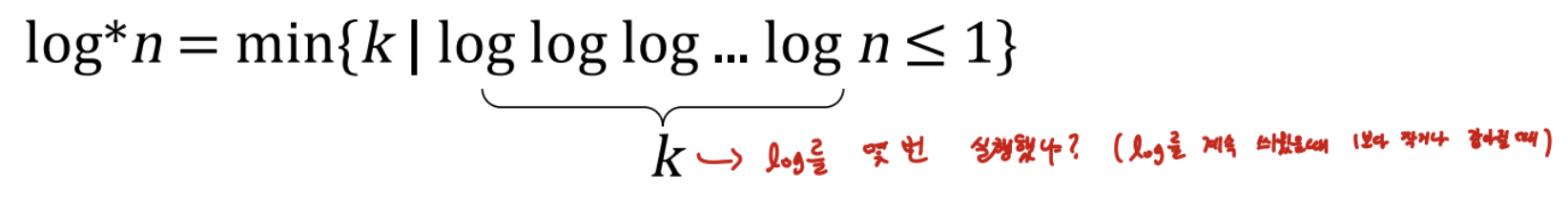
=> log*n은 사실상 상수라고 봐도 될 정도로 작음
따라서 사실상 Path Compression의 시간복잡도는 O(m)임!
Path Compression 할 때 두 번 반복하는 것을 피하려면?
Additional Issues

Root로 연결하는 대신에 조부모에 연결
=> 경로의 길이가 절반으로 줄어드는 효과
Path-halving의 경우 : 부모의 연결을 끊고 그 위의 조부모랑 연결함
(이 때 연결이 끊긴 부모는 추가적으로 뭘 하지 않고 넘어감)
Path-splitting의 경우 : 부모의 연결을 끊고 그 위의 조부모랑 연결함
(이 때 연결이 끊긴 부모도 같은 과정을 실행)
공통 조상이 있는 두 노드 u, v에 대해 union 연산을 빨리 끝내려면?

기존 find-set(u), find-set(v) 를 실행하면 Root까지 연산하지만
Rem's Algorithm은 공통 조상이 나타나면 연산 종료
1. 나의 부모가 항상 나보다 숫자가 적은 상태로 만든 후
2. 각 leaf에 포인터를 지정해놓고 시작
3. 부모를 확인하고 부모의 수가 더 큰쪽으로 포인터를 하나 올림
4. 이를 반복하다 양쪽 부모의 수가 같아지는 즉, 공통 조상이 나타나면 연산 종료
이 때 find-set을 쓰지 않으므로 Path Compression이 어렵기 때문에 Splicing 기법 적용
=> 포인터가 위로 올라갈 때 자기 부모와의 연결을 끊고 상대 포인터의 부모랑 연결
'🔥 Algorithm' 카테고리의 다른 글
| L12 - Single Source Shortest Paths (0) | 2024.11.28 |
|---|---|
| L11 - Minimum Spanning Trees (0) | 2024.11.26 |
| L09 - Greedy Algorithms (1) | 2024.11.03 |
| L07 - Selection (4) | 2024.10.13 |
| L06 - Non-comparison Sorting (2) | 2024.10.08 |
