국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Merge Sort
분할 정복(Divide and Conquer) 정렬 알고리즘임

=> 영역을 나눠서 각각 정렬하고 합치는게 Key Idea
(나뉜 영역을 재귀적으로 정렬)

Merging Two Sub-array

2개의 포인터를 이용하게 되는데 위 과정을 반복하여 나눠진 두 배열을 하나로 합친다
=> 두 Sub-array의 최솟값을 비교하고 더 작은값을 복사하는 방식

결국 Merge는 arr에 n개만큼을 정렬하여 값을 채우게됨
=> Θ(n) 만큼 연산을 필요로 하다는 것을 알 수 있음
Complexity Analysis of Merge Sort
mergesort(arr, l, l+n)의 시간복잡도를 점화식으로 표현해보면
반으로 분할하기 때문에 입력값이 n/2 인 mergesort 함수를 2회 호출하고 추가적인 Θ(n)인 merge 로직이 있으니
=> T(n) = 2T(n/2) + cn 이 된다
이는 이전 포스팅에서 다뤘던 Master Method에 따라
https://hanjungyo.tistory.com/80
L02 - Recurrences
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한 박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다 Complexity of Recursive Functions Algorithm1 은 팩토리얼을 재귀적으
hanjungyo.tistory.com
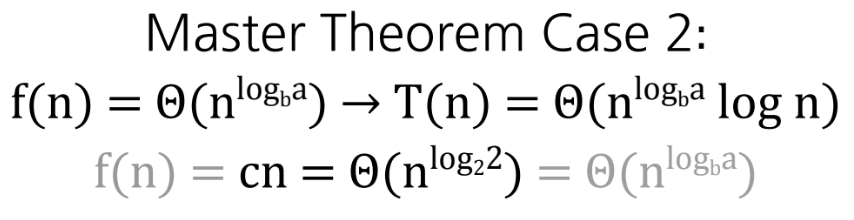
T(n) = Θ(nlogn) 이 된다
Merge sort는 기존 배열 arr의 크기인 n만큼의 임시 배열 tmp를 사용함
=> Θ(n)의 추가 메모리 사용
(추가적인 메모리 공간을 할당하여 정렬을 수행하는 알고리즘인 Out-of-place algorithm)
<-> 이와 반대로 주어진 배열 내 (추가 메모리 사용 x) 에서 정렬을 수행하는 알고리즘을 In-place algorithm이라고 함
(Bubble sort, Insertion sort, Selection sort, Quick sort ...)
Quicksort
Merge Sort와는 또 다른 분할 정복(Divide and Conquer) 정렬 알고리즘임

=> Pivot을 기준으로 영역을 나눠서 각각 정렬하는게 Key Idea
(나뉜 영역을 재귀적으로 정렬)
이 때 Pivot은 항상 제일 끝 값을 선택하고 (Lomuto Partition)
Pivot을 기준으로 왼쪽에는 Pivot 보다 작은값, 오른쪽에는 큰값이 위치하게 되는데 처음에는 정렬이 안되어 있어도 상관 X

Lomuto Partition
Lomuto Partition은 퀵 정렬에서 배열을 분할하기 위한 파티션 기법 중 하나임
=> 위에서 말했듯이 배열의 마지막 요소를 Pivot으로 선택한 후, 배열을 두 부분으로 나누어 Pivot보다 작은 값은 왼쪽에, Pivot보다 큰 값은 오른쪽에 배치하는 방식


=> 요약하자면 Pivot보다 작은 것은 왼쪽, 큰 것은 오른쪽으로 옮기고 Pivot 위치를 return 함
세부 설명
왼쪽 그림으로 보면 j가 Pivot 값보다 작으면 swap이 발생하는 것을 알 수 있음
(swap이 발생해도 i와 j가 동일하니까 왼쪽 그림의 1, 2, 3번 줄에서 변동이 없음)
만약 j로 배열을 돌던중 Pivot 보다 큰 값이 들어오게 되면 swap이 발생하지 않고 i가 증가하지 않는데 j는 for문을 도는 중이므로 하나 증가하게 됨
(왼쪽 그림 4번째 줄)
그렇게 계속 j로 돌면서 확인하다가 만약 Pivot 값보다 작은 값을 만나게 되면 swap이 발생하여 맨 처음 Pivot보다 큰 값을 발견했던 인덱스 자리와 체인지를 하여 Pivot보다 작은 것을 앞쪽(왼쪽) 으로 보내고 Pivot보다 큰 것은 뒤쪽(오른쪽)으로 옮김
(왼쪽 그림 7, 8번째 줄)
만약 j가 배열의 마지막 값을 가르키게 될 때 즉, Pivot값을 가르키게 되면 작성한 코드에 따라 Pivot과 같거나 작은 값에 포함되기 때문에 swap이 발생함
=> 이렇게 되면 swap이 발생하지 않은 값 중 제일 먼저 나왔던 Pivot 보다 큰 값의 인덱스 위치(변수 i가 가리키는 있는 곳)와 체인지를 함
(왼쪽 그림 9번째 줄)

이해가 안된다면 for문으로 배열을 도는동안 i와 j사이에 위치한 값들이 Pivot보다 큰 값들이라고 생각하고
마지막 인덱스 즉, Pivot값까지 for문을 돌게되는 순간 Pivot을 기준으로 왼쪽에는 Pivot보다 작은 값이, 오른쪽에는 Pivot 보다 큰 값들이 위치하게 됨
=> 이를 재귀적으로 계속하게되면 정렬 완료
Complexity Analysis of Quicksort
quicksort(arr, l, l +n)의 시간복잡도를 T(n)이라 하면
Best Case : partition 함수가 항상 절반으로 나누는 경우
partition 함수의 시간복잡도는 Θ(n)이고 입력 크기가 n/2인 quicksort 함수를 2회 호출하므로
T(n) = 2T(n/2) + cn => Θ(nlogn)
Worst Case : pivot이 배열내에서 항상 가장 큰 값이거나 가장 작은 값인 경우
Pivot이 맨 끝에 위치하게 될테니 Pivot을 기준으로 배열을 쪼개면 한쪽에는 아무것도 없고 반대쪽에 n-1개의 값이 들어간 배열이 생김
즉, 입력 크기가 n-1인 quicksort 함수를 1회 호출하므로
T(n) = T(n-1) + cn => Θ(n^2)
Average Case : 모든 경우의 평균인데
Pivot의 위치가 균등(uniform)함을 가정하면
Pivot의 위치에 따라
T(0) + T(n-1)
T(1) + T(n-2)
...
T(n-1) + T(0)
의 복잡도를 갖게되므로 (1/n 확률로)
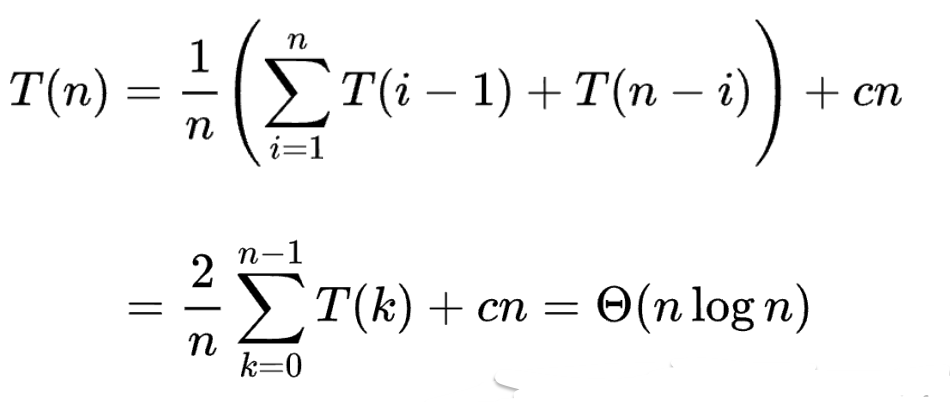
증명 방법
sorting 알고리즘의 하한은 Ω(nlogn) 이 증명되어 있어서 상한만 증명하면 된다
T(n) = O(nlogn)
T(n) <= c * nlogn for all n0 <= n
위 식을 풀어서 적어보면
2/n ( T(1) + T(2) + T(3) + T(4) + ... T(n-1) ) + C0n + C1 ... T(0)은 상수이므로 밖으로 뺌
= 2c/n ( 1log1 + 2log2 + 3log3 + 4log4 + ... + (n-1)log(n-1) ) + C0n + C1
<= 2c/n ( 1logn + 2logn + 3logn + 4logn + ... + (n-1)logn ) + C0n + C1
= 2c/n ( 1 + 2 + 3 + 4 + ... + (n-1) )logn + C0n + C1
= (2c/n) * (n(n-1)/2) logn + C0n + C1
= c(n-1) logn + C0n + C1
= cnlogn - clogn + C0n + C1
<= cnlogn (충분히 큰 c를 선택하면 됨)
Merge Sort는 인덱스를 기준으로 나누고 Quicksort는 데이터를 기준으로 나눔
'Algorithm' 카테고리의 다른 글
| L06 - Non-comparison Sorting (2) | 2024.10.08 |
|---|---|
| L05 - Heapsort (2) | 2024.10.06 |
| L03 - Basic Sorting Algorithms (1) | 2024.09.25 |
| L02 - Recurrences (1) | 2024.09.17 |
| L01 - Algorithm Analysis (1) | 2024.09.14 |
