국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Lower Bounds of Comparision Sorting
비교 기반 정렬 알고리즘 (Comparision sort) 에서 Worst case에 O(nlogn) 보다 빠른게 존재할까?
정렬 문제의 상한은 O(nlogn) 임
=> quicksort 라는 O(nlogn) 알고리즘이 존재하기 때문
정렬 문제의 하한은 Ω(n log n) 임
=> 모든 알고리즘이 Ω(n log n) 인 것을 증명해야함
Comparison Sort를 Decision Tree로 추상화 가능함
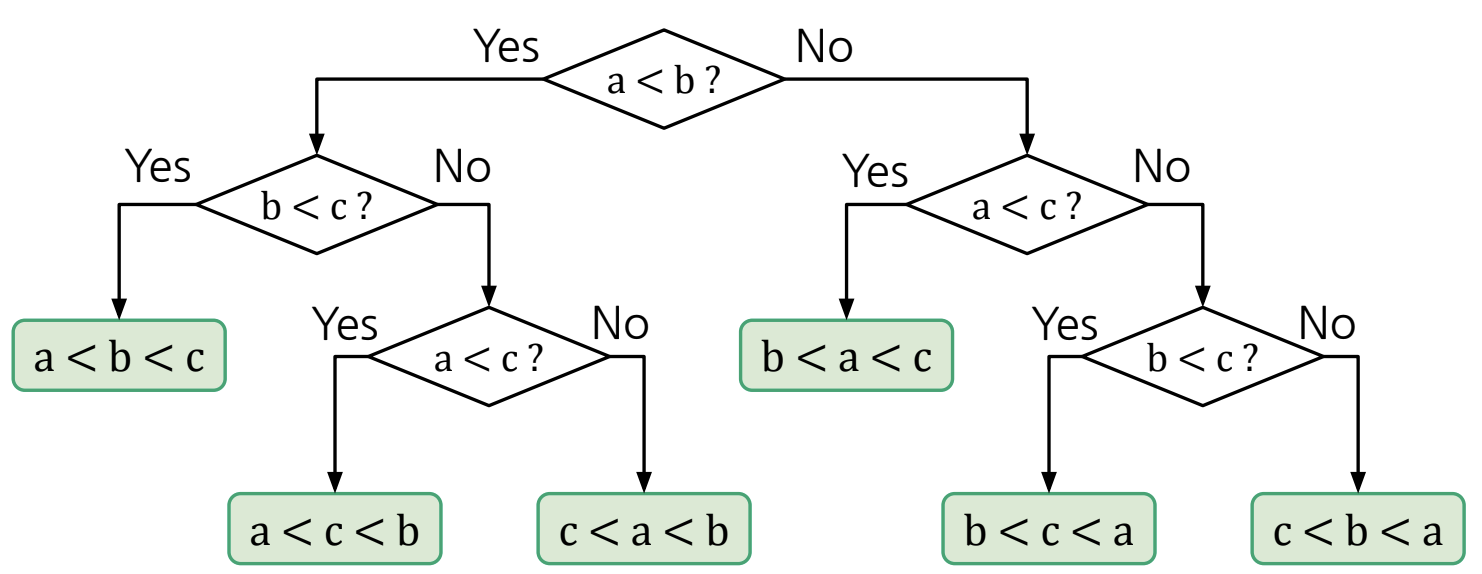
위 그림 처럼 모든 sort의 process를 Decision Tree 형태로 추상화가 가능함!
=> Tree-height의 의미는 비교하는 횟수로 볼 수 있음!
(Non-leaf nodes는 비교연산)
그럼 n개의 서로 다른 값을 정렬하는 모든 알고리즘의 Decision Tree가 Ω(n log n)의 Height를 갖는지 확인하면 하한을 구할 수 있음
DecisionTree의 Leaf node 수 = n!
(만약 1, 2, 3을 정렬한다고 했을 때 나올 수 있는 정렬의 수는 3! = 3 * 2 * 1 인 6가지임)
그렇다면 Decision Tree의 최소 Height? (최악의 깊이가 최소인 경우 = 아주 균등한 트리가 만들어 졌을 때)
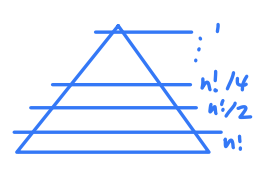
위 그림에서 1 = n! / 2^k 이므로 트리의 높이 k = log_2(n!) 임!
즉, 가장 균등할 때의 height 가 log_2(n!) 이므로
Tree Height 인 h는 h >= log_2(n!) 라고 볼 수 있음
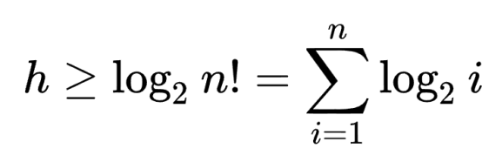
log n! = log n * log (n - 1) * ... log 1 = log n + log (n - 1) + ... + log 2 + log 1 이므로
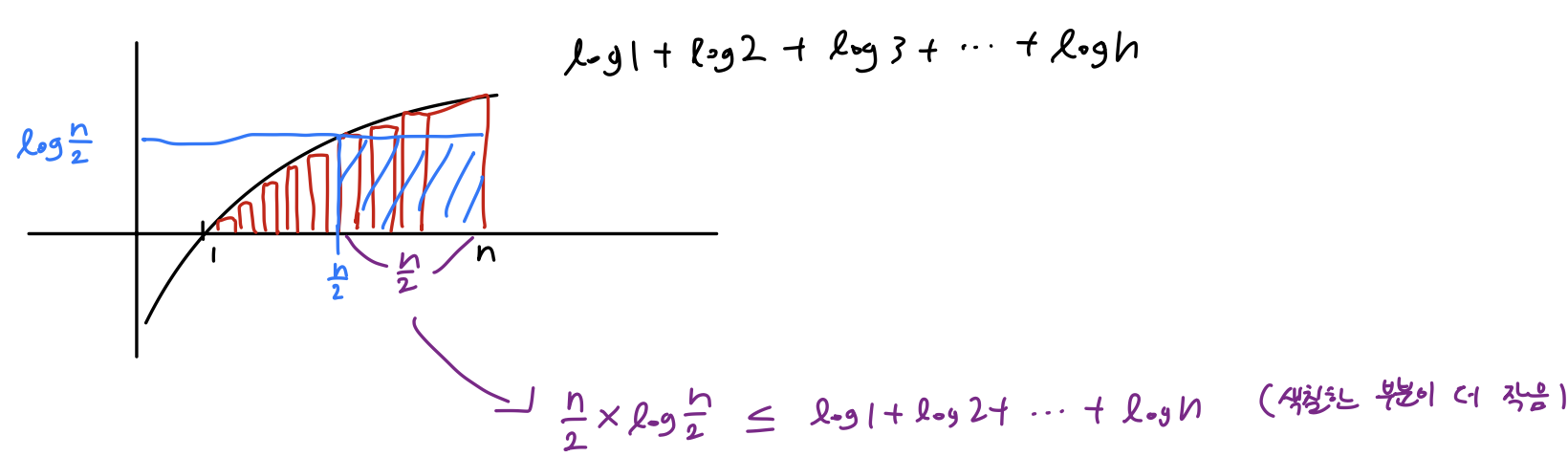
위와 같은 그림을 그려볼 수 있음

즉, 이런식으로 표현이 가능하고
이는 곧 Ω(nlogn) 을 의미함!
(상수 사라지므로)
정리를 해보면
모든 비교 기반 알고리즘은 Decision Tree의 형태로 만들 수 있는데
이 Decision Tree의 Height가 최소 n/2 log_2 (n/2) 보다는 크다는걸 증명함
따라서, 어떤 비교 기반 알고리즘이라고 하더라도 Decision Tree의 Height는 Ω(nlogn) 보다는 클 수 밖에 없음!!
Non-comparison Sorting
최악의 경우 정렬 시간이 Θ(n log n) 보다 빠를 수 없을까?
비교 정렬 알고리즘의 경우 원소의 상대적 대소 관계만 고려함
=> 원소의 분포나 자릿수 등을 고려한다면 더 빠를 수 있음
Counting Sort : 값들이 r 이하의 음이 아닌 정수일 때
Radix Sort : 값들이 모두 k 자릿수 이하의 음이 아닌 정수일 때
Counting Sort
조건 : 값들이 r 이하의 음이 아닌 정수일 때
(중복을 허용)
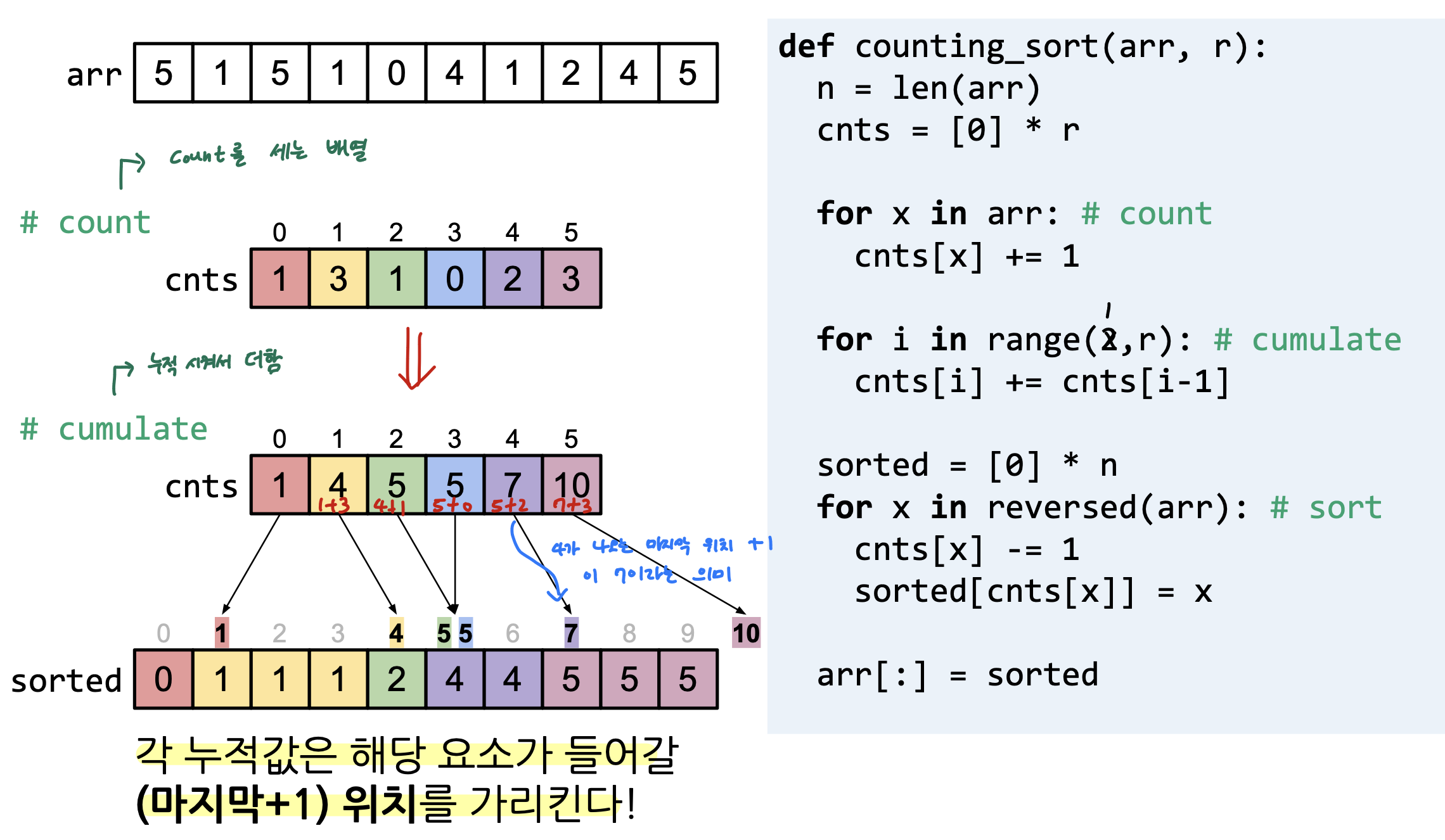
Key idea는 각 값의 개수를 세어, 값마다 들어갈 위치를 미리 계산하는 것이다!
pseudocode 를 함께 살펴보면
우선 주어진 배열에서 각 값의 개수를 세어 cnts 배열에 저장하고
cnts 배열의 count 값을 이전 count 값에 누적시켜서 계속 더하고 있음
=> 이때 cnts 배열의 각 누적값은 해당 요소가 들어갈 마지막 위치의 + 1을 가리킴
그렇다면 정렬은 어떻게?
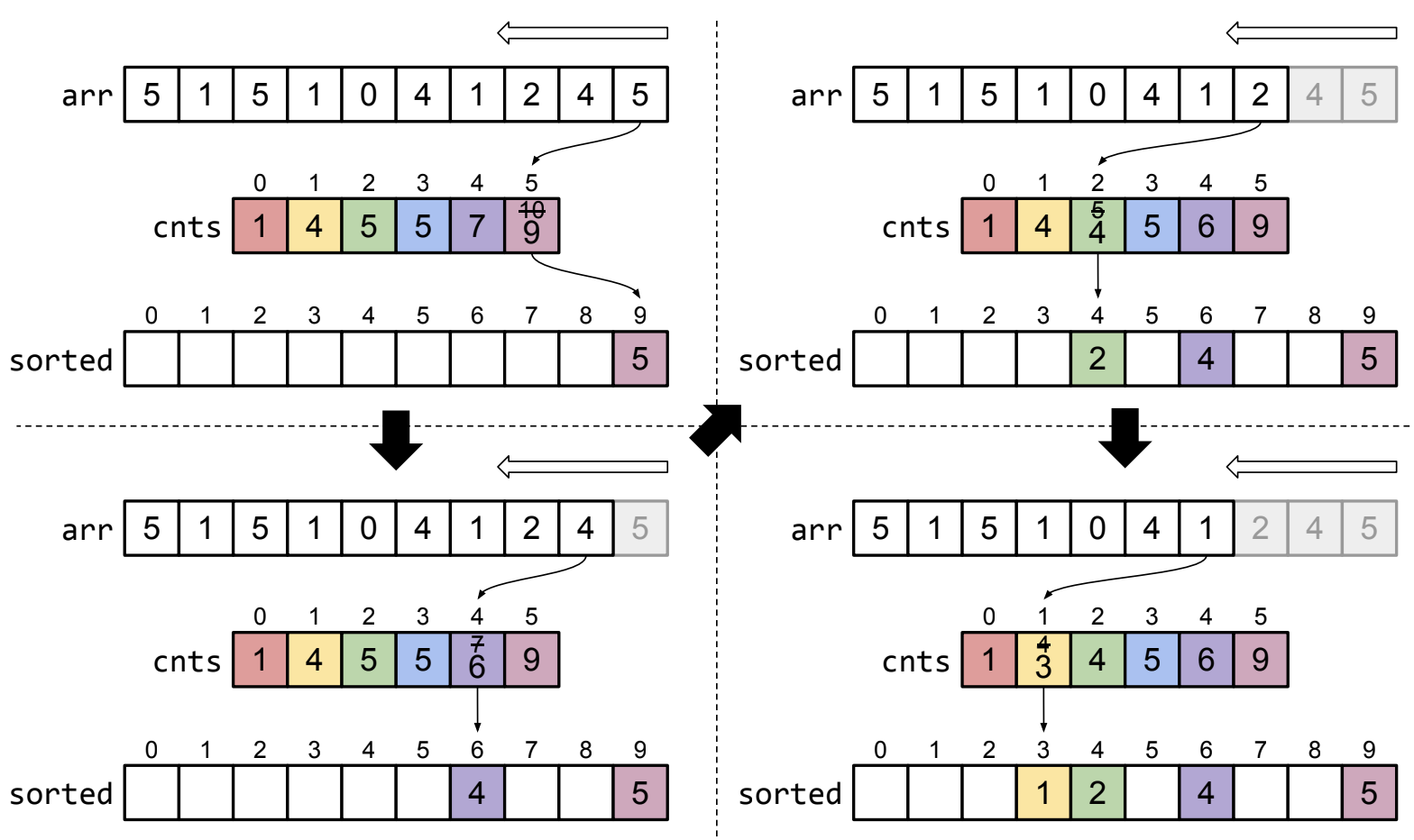
정렬해야 할 배열을 뒤에서부터 거꾸로 scan 하며 미리 정의해둔 sorted 배열에 해당 요소의 자리를 찾아서 넣어줌
(위에서 말했듯이 count를 세는 배열에서의 누적값이 요소가 들어갈 마지막 위치의 +1을 가리키는 원리로 자리를 찾을 수 있음)
즉, 위 그림에서 요소 5의 누적값이 10이면 이게 마지막 위치의 +1을 가리키므로 9번 자리에 요소 5를 쓰면됨
이 때 해당 요소의 누적값을 -1 해주면 정렬해야 할 배열에서 다음에 해당 요소가 또 나왔을 경우 (중복 값 허용이므로) 전에 해당 요소를 썼던 곳 보다 한 칸 앞에 적어줄 수 있음
이런식으로 반복하며 정렬해야 할 배열의 처음 등장하는 요소까지 거꾸로 scan을 하게 되면 sorted 배열에 원하는대로 정렬이 되어 있음!
Complexity Analysis of Counting Sort

여기서 r은 배열의 최댓값으로 위에서 나온 Counting Sort 예제를 기준으로 0~5까지의 숫자가 있으니 r은 6이 됨!
count 하는 부분에서의 시간 복잡도는 Θ(n) 으로 볼 수 있음
=> 어쩌피 주어진 배열을 한 번 sacn 하면서 count 하므로
cumulate 하는 부분에서의 시간 복잡도는 Θ(r) 로 볼 수 있음
=> count를 세는 배열에서 이전 누적값을 차례로 더하는 과정을 r - 1 번 수행하므로
sort 하는 부분에서의 시간 복잡도는 Θ(n) 로 볼 수 있음
=> 주어진 배열을 거꾸로 한 번 scan 하는 것이므로
=> 추가적으로 정렬해놓은 sorted 배열을 원래의 배열 arr에 복사하는 과정도 Θ(n) 임
최악의 경우로 생각했을 때 시간 복잡도가 Θ(r + n) 이고 보통 r이 n보다 작다고 보니까 Θ(n)이 된다!
r이 nlogn 이라면 Θ(n log n) 이므로 써야할 메리트가 없음!
Radix Sort
조건 : 값들이 모두 k 자릿수 이하의 음이 아닌 정수 일 때
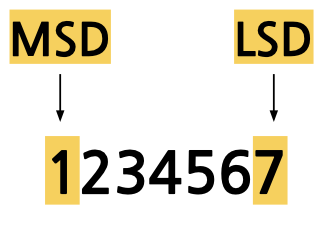
Key Idea : 낮은 자릿수(LSD) 부터 높은 자릿수 (MSD) 순서대로 자릿수를 기준으로 안정 정렬(stable sort)
Stable sort 란 같은 값들간 상대적인 순서를 유지하며 정렬하는 것임
ex. Bubble sort, Insertion sort, Merge sort, Counting sort

위와 같이 LSD 부터 시작하여 차례로 안정 정렬을 실행함
하지만, 안정 정렬을 할 때 Bubble Sort 같은 알고리즘은 n^2 만큼 걸리므로
=> 이 때 Counting Sort 를 사용할 수 있음
(10진수 기준으로 0~9까지의 숫자만 사용하므로 문제될게 없음)
아까 말했듯이 자릿수를 기준으로 stable sort를 진행하기 때문에 그 다음 자릿수에서 겹치는 숫자가 있더라도 이미 낮은 자릿수에서 정렬을 했으므로 순서가 유지됨!

각 자릿수로 정렬할 때 Counting Sort를 활용하는데 r이 상수면 Θ(n + r) = Θ(n)로 매우 효율적임!!
=> code를 살펴보면 Counting Sort와 비슷하지만 rtok 를 이용하여 LSD 부터 MSD까지 차례로 (안정)정렬을 적용함
Complexity Analysis of Radix Sort
Θ(r + n)인 counting sort를 k번 반복하므로
=> 최악의 경우 시간 복잡도는 Θ(rk + nk)로 볼 수 있음!
(보통 r, k가 상수가 되므로 Θ(n)으로 볼 수 있음)
주어진 값들이 모두 다를 경우 복잡도는?
우선 생각해봐야할 것은 중복을 허용하지 않는다고 했을 때 n이 1000만이면 자릿수의 최댓값은 log_10(n) = 7 자리가 됨
즉, k = log_r(n)
(10진수라고 했을 때 r은 9 + 1 = 10 이므로 log_10 으로 계산했음)
따라서 Radix Sort의 복잡도 Θ(rk + nk) 에서 k의 자리에 log(n)을 넣으면
Θ(rk + nk) = Θ(rlog_r(n) + nlog_r(n))
여기서 r이 상수라면 Θ(n log n) 로 볼 수 있음
결국 Radix Sort도 비교기반 정렬이 아니더라도 중복을 허용하지 않는다면 시간 복잡도가 Θ(n log n) 가 됨!
'🔥 Algorithm' 카테고리의 다른 글
| L09 - Greedy Algorithms (1) | 2024.11.03 |
|---|---|
| L07 - Selection (4) | 2024.10.13 |
| L05 - Heapsort (2) | 2024.10.06 |
| L04 - Merge Sort & Quicksort (2) | 2024.09.27 |
| L03 - Basic Sorting Algorithms (1) | 2024.09.25 |
