국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Complexity of Recursive Functions

Algorithm1 은 팩토리얼을 재귀적으로 나타내고 있고
Algorithm2 는 탐색 범위를 반으로 나누어 해당 숫자를 탐색하고 있음
그럼 복잡도는 어떻게 될까..?
바로 복잡도를 구하기는 힘들고 우선 복잡도 함수의 점화식 (Recurrence Relation)을 구해볼 수 있음

=> 이는 복잡도 함수를 재귀적으로 정의한 식
Solving Recurrences
복잡도를 구하고 싶은데 점화식은 또 어떻게 풀 수 있을까..?
점화식을 푼다 = 점화식을 해석적 해로 변환
=> 해석적 해(Closed solution) 란 유한한 수의 기본연산으로 표현한 식

점화식에 차례차례 n을 줄여가며 대입하면 해석적 해를 구할 수 있음
=> 너무 고단한 작업임
점화식을 직접 대입하지 않고 어떻게 풀 수 있을까?
Substitution Method (추정 후 증명)
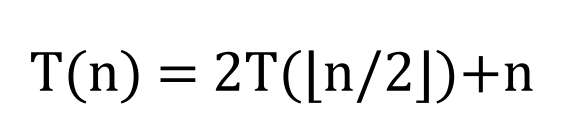
위와 같은 점화식이 있을 때 Substitution Method를 이용해보면
1. 추측하기 : T(n) = O(nlogn) 일 것이다.
2. 대입하여 증명하기 (수학적 귀납법 사용) : n >= n0 일 때 T(n) <= c * nlogn 인 c와 n0 찾기
과정을 거쳐야함
원래는 n0 <= k < n 인 모든 k에 대해 T(k) <= c * klogk 임을 보여주는 Base case를 증명해야함
(n0 = 1은 log 함수의 정의가 문제를 일으키므로 사용 X)
하지만, a가 상수일 때 T(a)는 Θ(1) 이므로 (종료가 되는 알고리즘이라면 상수로 볼 수 있기 때문), 귀납적 증명 시 Base case를 증명하지 않아도 됨!
수학적 귀납법을 이용해보면
Induction case
n = 1, 2, ..., k 일 때 T(n) <= c * nlogn 을 만족한다 가정하고
n = k + 1 일 때도 T(n) <= c * nlogn 임을 증명
T(n) = 2T(⌊n/2⌋) + n
<= 2c⌊n/2⌋log⌊n/2⌋ + n
<= cn log (n/2) + n ... ⌊n/2⌋ <= n/2 이므로
= cn log n - cn + n
<= cn log n ... -cn + n 이 음수가 되게 설정한다면
따라서, T(n) = O(nlogn)
Substitution Method의 여러 case
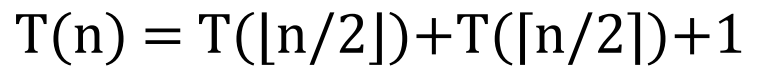
T(n) = O(n) 라고 추측하고 Substitution Method를 이용해보면
T(n) <= cn 임을 증명해야 하는데 T(n) <= cn + 1이 나와서 증명이 실패함
=> 이럴 경우 T(n) <= cn - b 를 증명하면 됨
왜냐면 T(n) = O(n - k) = O(n) 임을 증명하면 되니까
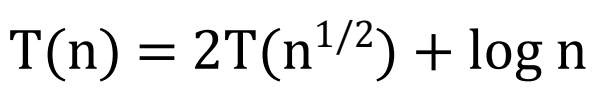
이런 경우는 log n = m 으로 두고, m에 대한 수식으로 변경하여 점화식을 풀 수 있음
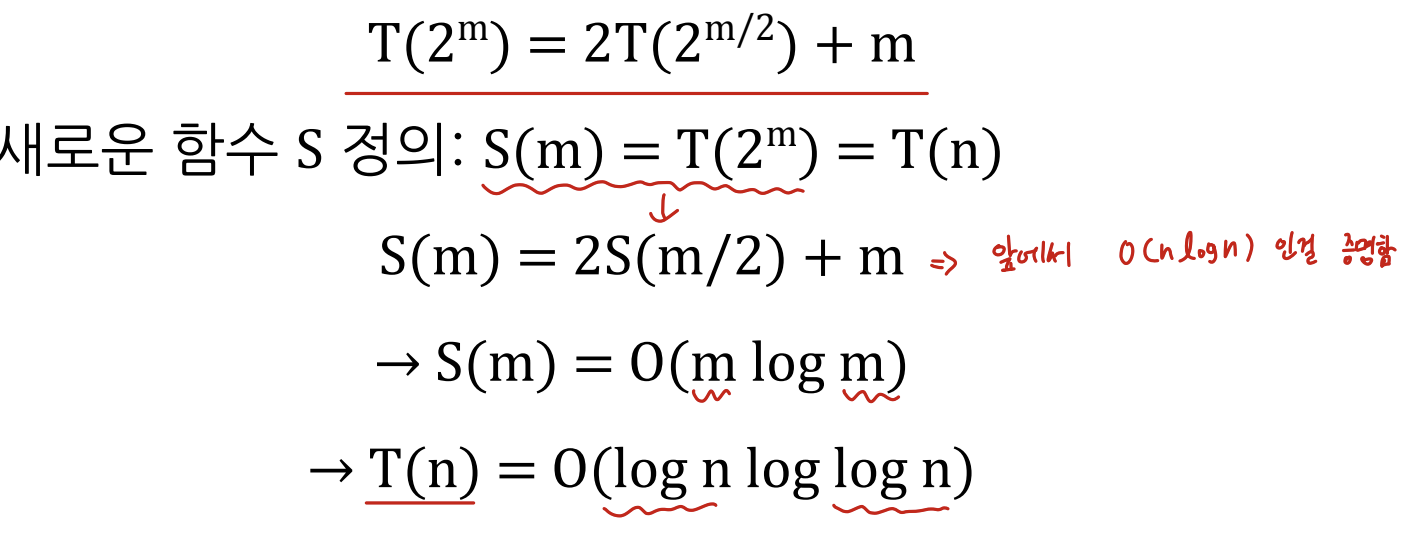
Recursion-Tree Method (반복 전개, Tree로 표현)
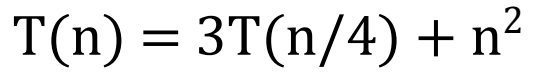
위 점화식을 전개하여 풀면
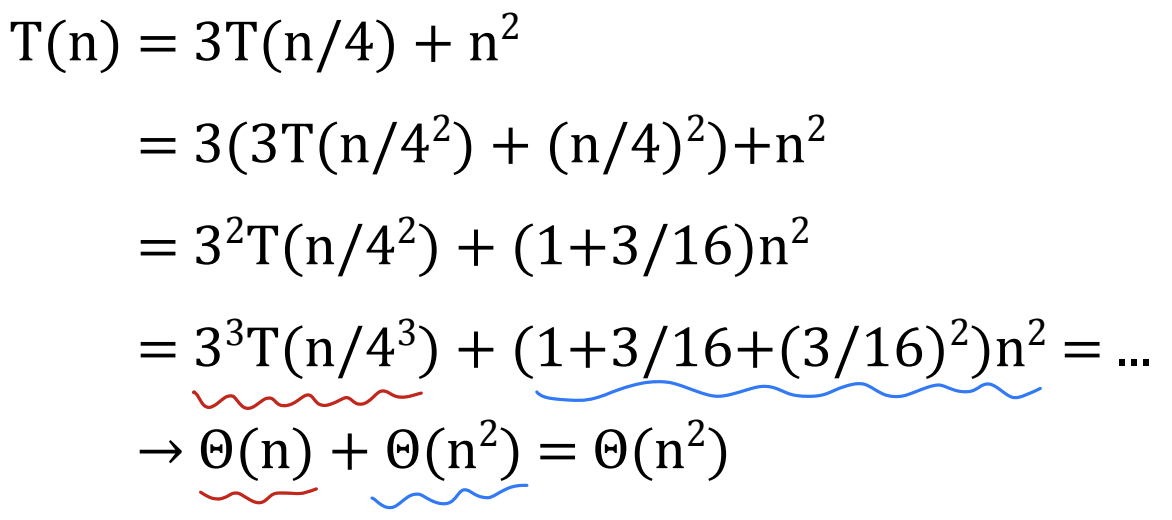
이런식으로 전개가 될텐데 이 전개 과정을 Recursion Tree로 표현하는 것이 Recursion-tree Method 임!
이 때 각 정점은 각 하위문제의 복잡도로 표현됨
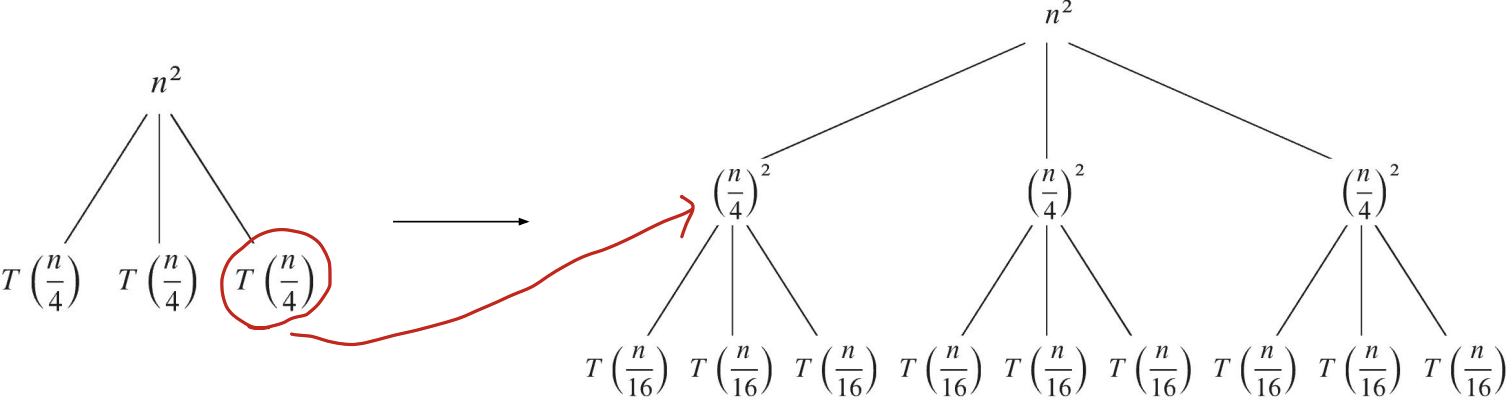
=> T(n) = 3T(n/4) + n^2 에서 n^2가 얼마나 계산되는지 트리의 노드로 적어 놓음
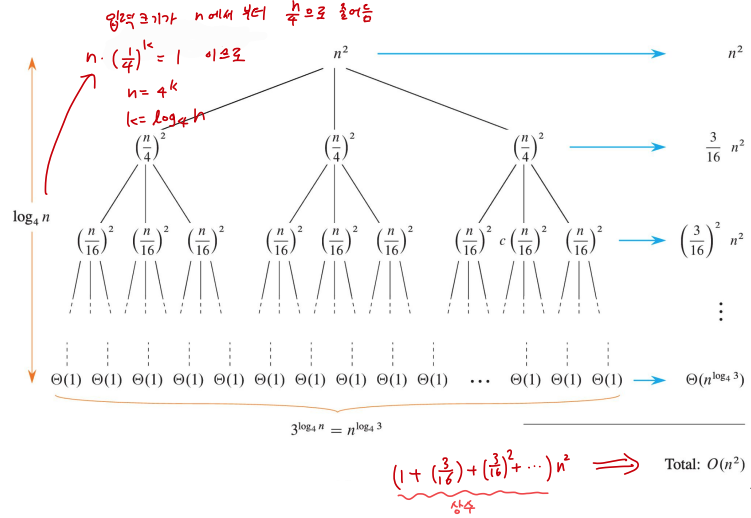
트리의 깊이가 log4(n) 인데 이는 문제 크기가 재귀 호출이 한 단계 진행될 때 마다 1/4 로 줄어들기 때문에 n이 n/4로 줄어드는 과정을 k번 반복해서 1에 도달하는 깊이인 log4(n) 임
트리의 깊이가 항상 동일하게 나오는건 아니라는 사실을 알고 있어야함!
Master Method (Master theorem 이용)
T(n) = aT(n/b) + f(n) 와 같은 형태의 점화식은 Master Theorem을 이용하여 간단히 풀 수 있음!
(a >= 1 와 b > 1는 상수)
Master Theorem은 세 가지 경우로 볼 수 있는데
n^logb(a) 에 대해 상대적으로
f(n)이 작을때, 적당할 때, 클 때의 경우로 나눌 수 있음

예시로 T(n) = 9T(n/3) + n 는 Master Method의 형태와 일치하여
a = 9, b = 3이기 때문에 n^log3(9) = n^2 이 비교대상이 되고, f(n) = n 이므로
case 1에 부합하여 Θ(n^log3(9)) = Θ(n^2) 이 된다!
'🔥 Algorithm' 카테고리의 다른 글
| L05 - Heapsort (2) | 2024.10.06 |
|---|---|
| L04 - Merge Sort & Quicksort (2) | 2024.09.27 |
| L03 - Basic Sorting Algorithms (1) | 2024.09.25 |
| L01 - Algorithm Analysis (1) | 2024.09.14 |
| 시간복잡도와 디버깅 (3) | 2024.01.17 |
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
Complexity of Recursive Functions

Algorithm1 은 팩토리얼을 재귀적으로 나타내고 있고
Algorithm2 는 탐색 범위를 반으로 나누어 해당 숫자를 탐색하고 있음
그럼 복잡도는 어떻게 될까..?
바로 복잡도를 구하기는 힘들고 우선 복잡도 함수의 점화식 (Recurrence Relation)을 구해볼 수 있음

=> 이는 복잡도 함수를 재귀적으로 정의한 식
Solving Recurrences
복잡도를 구하고 싶은데 점화식은 또 어떻게 풀 수 있을까..?
점화식을 푼다 = 점화식을 해석적 해로 변환
=> 해석적 해(Closed solution) 란 유한한 수의 기본연산으로 표현한 식

점화식에 차례차례 n을 줄여가며 대입하면 해석적 해를 구할 수 있음
=> 너무 고단한 작업임
점화식을 직접 대입하지 않고 어떻게 풀 수 있을까?
Substitution Method (추정 후 증명)
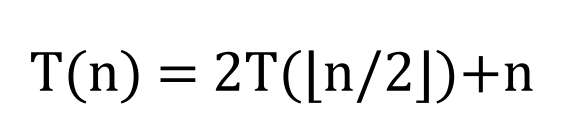
위와 같은 점화식이 있을 때 Substitution Method를 이용해보면
1. 추측하기 : T(n) = O(nlogn) 일 것이다.
2. 대입하여 증명하기 (수학적 귀납법 사용) : n >= n0 일 때 T(n) <= c * nlogn 인 c와 n0 찾기
과정을 거쳐야함
원래는 n0 <= k < n 인 모든 k에 대해 T(k) <= c * klogk 임을 보여주는 Base case를 증명해야함
(n0 = 1은 log 함수의 정의가 문제를 일으키므로 사용 X)
하지만, a가 상수일 때 T(a)는 Θ(1) 이므로 (종료가 되는 알고리즘이라면 상수로 볼 수 있기 때문), 귀납적 증명 시 Base case를 증명하지 않아도 됨!
수학적 귀납법을 이용해보면
Induction case
n = 1, 2, ..., k 일 때 T(n) <= c * nlogn 을 만족한다 가정하고
n = k + 1 일 때도 T(n) <= c * nlogn 임을 증명
T(n) = 2T(⌊n/2⌋) + n
<= 2c⌊n/2⌋log⌊n/2⌋ + n
<= cn log (n/2) + n ... ⌊n/2⌋ <= n/2 이므로
= cn log n - cn + n
<= cn log n ... -cn + n 이 음수가 되게 설정한다면
따라서, T(n) = O(nlogn)
Substitution Method의 여러 case
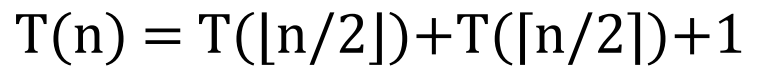
T(n) = O(n) 라고 추측하고 Substitution Method를 이용해보면
T(n) <= cn 임을 증명해야 하는데 T(n) <= cn + 1이 나와서 증명이 실패함
=> 이럴 경우 T(n) <= cn - b 를 증명하면 됨
왜냐면 T(n) = O(n - k) = O(n) 임을 증명하면 되니까
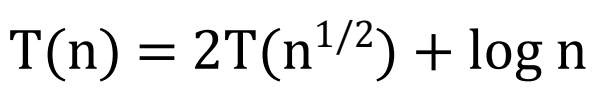
이런 경우는 log n = m 으로 두고, m에 대한 수식으로 변경하여 점화식을 풀 수 있음
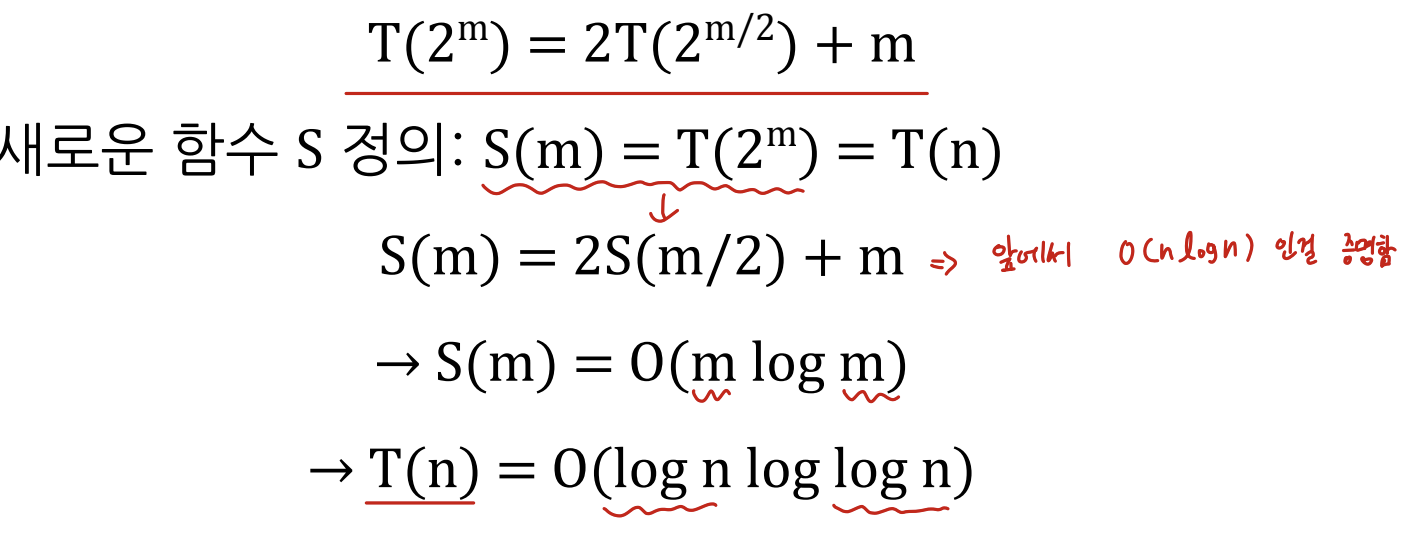
Recursion-Tree Method (반복 전개, Tree로 표현)
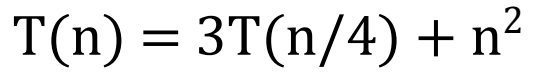
위 점화식을 전개하여 풀면
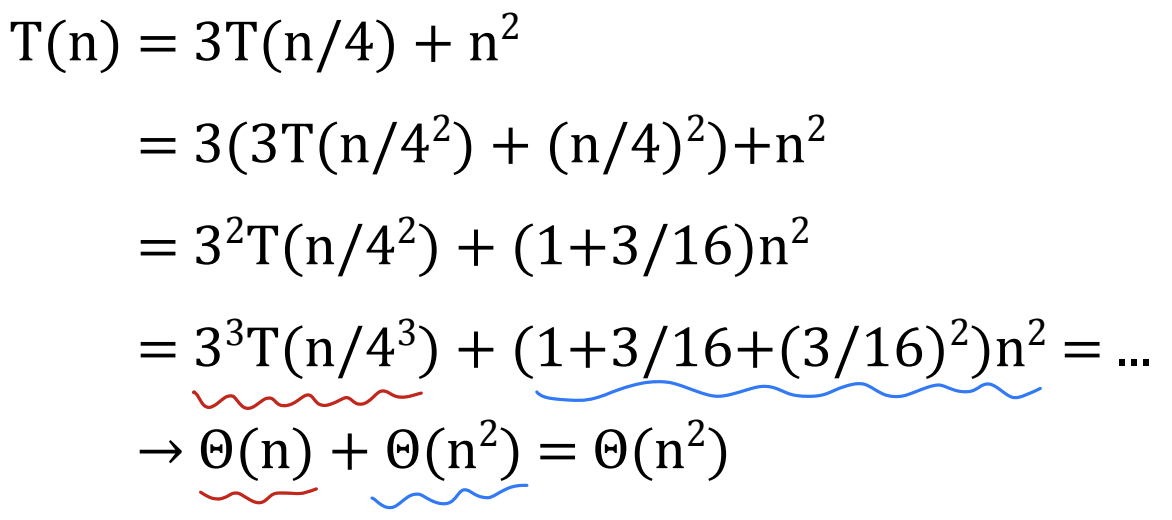
이런식으로 전개가 될텐데 이 전개 과정을 Recursion Tree로 표현하는 것이 Recursion-tree Method 임!
이 때 각 정점은 각 하위문제의 복잡도로 표현됨

=> T(n) = 3T(n/4) + n^2 에서 n^2가 얼마나 계산되는지 트리의 노드로 적어 놓음

트리의 깊이가 log4(n) 인데 이는 문제 크기가 재귀 호출이 한 단계 진행될 때 마다 1/4 로 줄어들기 때문에 n이 n/4로 줄어드는 과정을 k번 반복해서 1에 도달하는 깊이인 log4(n) 임
트리의 깊이가 항상 동일하게 나오는건 아니라는 사실을 알고 있어야함!
Master Method (Master theorem 이용)
T(n) = aT(n/b) + f(n) 와 같은 형태의 점화식은 Master Theorem을 이용하여 간단히 풀 수 있음!
(a >= 1 와 b > 1는 상수)
Master Theorem은 세 가지 경우로 볼 수 있는데
n^logb(a) 에 대해 상대적으로
f(n)이 작을때, 적당할 때, 클 때의 경우로 나눌 수 있음

예시로 T(n) = 9T(n/3) + n 는 Master Method의 형태와 일치하여
a = 9, b = 3이기 때문에 n^log3(9) = n^2 이 비교대상이 되고, f(n) = n 이므로
case 1에 부합하여 Θ(n^log3(9)) = Θ(n^2) 이 된다!
'🔥 Algorithm' 카테고리의 다른 글
| L05 - Heapsort (2) | 2024.10.06 |
|---|---|
| L04 - Merge Sort & Quicksort (2) | 2024.09.27 |
| L03 - Basic Sorting Algorithms (1) | 2024.09.25 |
| L01 - Algorithm Analysis (1) | 2024.09.14 |
| 시간복잡도와 디버깅 (3) | 2024.01.17 |
