국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
NP-Completeness 개요
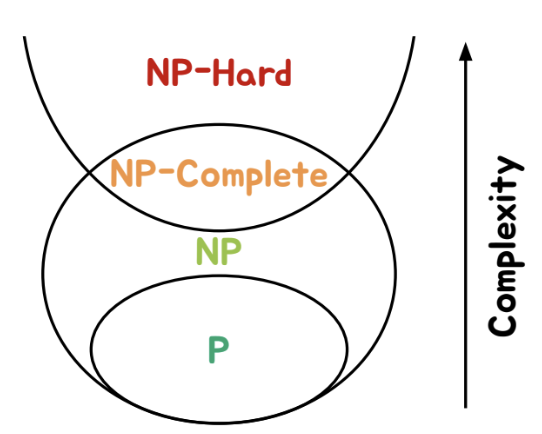
P : 다항시간에 풀 수 있는 결정 문제 집합
NP : 비결정론적으로 다항시간에 풀 수 있는 결정 문제 집합
=> 답을 다항시간에 검증할 수 있는 문제
(다항시간에 검증할 수 있으면 NP 문제)
NP-Hard : 모든 NP 문제에서 다항시간 변환되는 문제 집합
=> 검증이 안될 수 도 있음 (NP - Complete와의 차이)
NP-Complete : NP-Hard 이면서 NP인 문제
(결국 NP이기에 yes/no의 결정문제 집합임)
NP-Hard 증명 방법
문제 A가 NP-Hard 임을 증명하는 방법에는 2가지가 있음
1. NP-Hard 정의에 따라 모든 NP문제를 문제 A로 다항시간 변환해봄
=> 이건 사실상 불가능
(모든 NP 문제를 일일이 변화해야함)
2. NP-Hard인 문제 B를 문제 A로 다항시간 변환해봄
=> NP-Hard인 문제 B를 문제 A로 다항시간 변환할 수 있으면 문제 A는 NP-Hard임
문제 A가 NP-Hard임을 증명하고 NP임도 증명
NP-Complete 증명 방법
문제 A가 NP-Hard 임을 증명하고 NP임도 증명하면됨
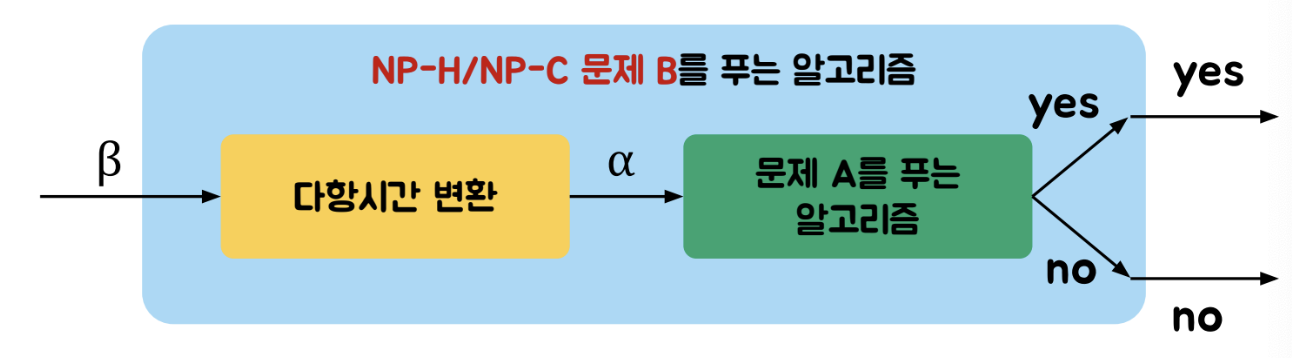
알려진 NP-Hard 문제에서 다항시간 변환해서 NP-Hard 임을 증명하고
답이 다항시간에 검증되는지 확인하여 NP임도 증명하면됨
NP-Complete 문제들
NP-Complete 문제들은 모두 동일하게 어려움
=> 다항시간 알고리즘이 아직 알려지지 않음
(P = NP가 증명 X)
NP-Complete 문제는 NP-Hard 정의에 따라 서로 변환이 가능함
=> NP-Hard는 모든 NP문제를 다항 시간 내에 풀 수 있음을 의미하는데 결국 모든 NP-Complete 문제는 NP이기에 서로 변환 가능
NP-Complete가 가지는 의미
일단 현재는 P = NP가 증명되지 않았기에 NP 문제를 다항시간에 푸는 알고리즘은 아직 모름
(많은 사람들이 실패함)
만약 P = NP라면 NP-Complete도 P임
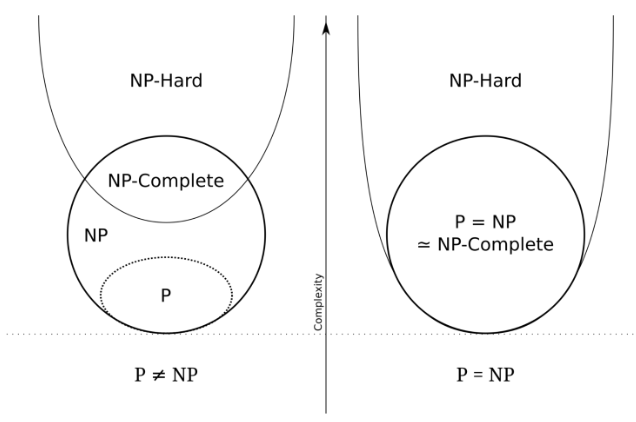
만일 NP-Complete 문제 중 단 하나만이라도 다항시간 알고리즘을 발견하면, 모든 NP문제를 다항시간에 풀 수 있음
=> 모든 NP 문제는 NP-Complete 문제로 변환되기 떄문
TSP = NP-Complete?
TSP는 이전에 다뤘었는데 외판원 순환 문제라고해서 모든 정점을 방문하고 시작 정점으로 돌아오는 길이 K이하의 최단 경로가 존재하는가? 에 대한 문제임
TSP가 NP-Complete임을 증명하려면
1. NP-Hard임을 증명
=> HAM-CYCLE을 다항시간 변환
(HAM-CYCLE은 NP-Hard임)
2. NP임을 증명
=> 어떤 순환 경로가 답으로 주어지면
- 이 경로가 모든 노드를 지나는지
- 경로의 합이 K이하인지 다항시간에 확인가능
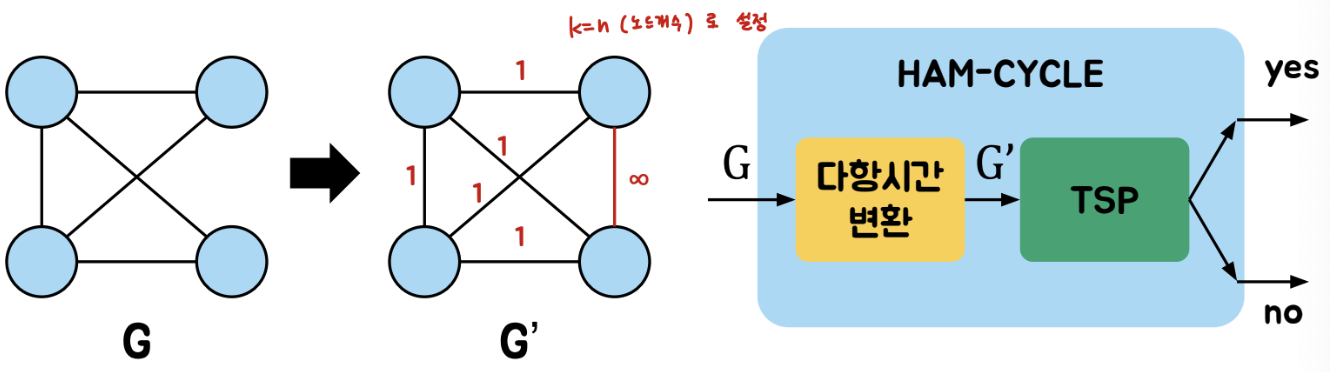
NP-Complete인 HAM-CYCLE을 변환하여 증명
=> HAM-CYCLE의 입력 G를 TSP의 입력 G'로 변환
- G의 모든 간선의 가중치를 1로 설정
- 없는 간선은 생성하여 가중치를 무한대로 설정
- 정점의 수가 n일 때, O(n^2)의 시간 필요
K=n인 TSP 문제의 정답은 HAM-CYCLE의 정답과 동일하므로
Longest Path = NP-Complete?
LONGEST-PATH는 두 점을 잇는 길이가 K 이상인 단순 경로를 찾는 문제
질문은 s에서 t로 가는 길이가 K 이상인 단순 경로가 존재하는가?
(단순 경로란 같은 정점이 두 번 이상 반복되지 않는 경로)
Longest Path는 NP 인가?
한 경로가 답으로 제시되었을 때 올바른 답인지 검증하는데 다항 시간이 걸림
- s에서 t로 끝나는가? -> O(1)
- 경로가 단순 경로인가? -> O(n)
- 경로의 길이가 K 이상인가? -> O(n)
Longest Path는 NP-Hard 인가?
NP-Complete인 Hamiltonian Path 문제를 다항시간 변환하여 증명
HAM-PATH-2-POINTS는 두 점을 잇는 hamiltonian path를 찾는 문제임
=> s에서 t로 가는 hamiltonian path가 존재하는가?
(hamiltonian path는 그래프의 모든 정점을 한 번씩 지나는 경로임)
HAM-PATH-2-POINTS => LONGEST-PATH
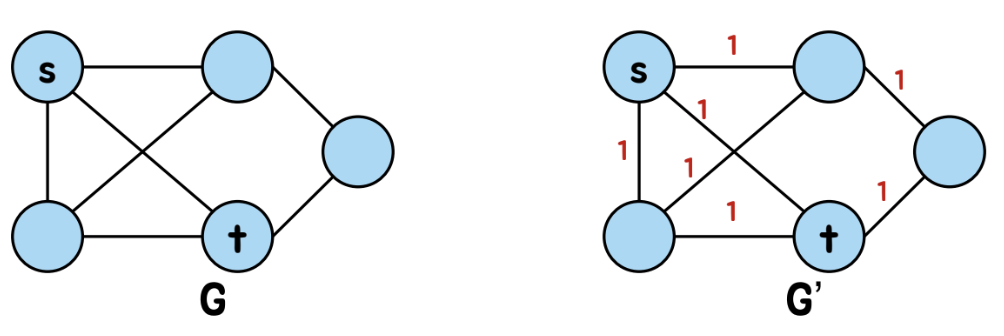
HAM-PATH 의 입력 G를 LONGEST-PATH 입력 G'으로 변환
G의 모든 간선에 weight를 1로 부여하여 G' 생성하고
(변환시간은 O(n^2))
G',s,t를 입력받는 LONGEST-PATH 문제의 답 (K = n - 1 일 때) 이
G,s,t를 입력받는 HAM-PATH-2-POINTS 문제의 답과 동일함
NP-Hardness of Optimization Problems
다항시간 변환의 정의를 확장하여 최적화 문제에 적용
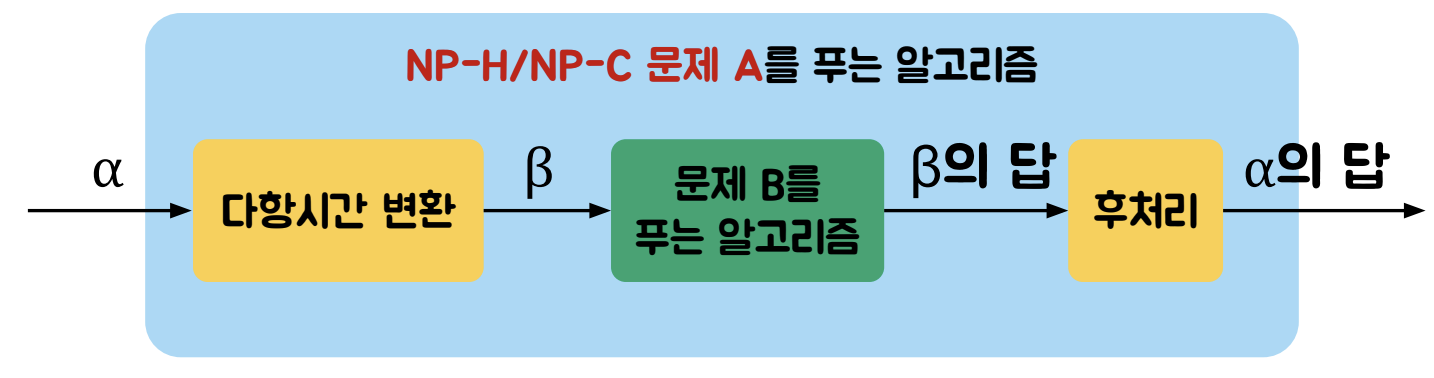
=> 이전에 다뤘던 다항시간 변환의 정의를 확장할 수 있음
- 변환은 다항시간에 이뤄진다.
두 사례의 답이 일치한다.
=> β의 답을 이용하여 α의 답을 구할 수 있다.
[TSP] : TSP 문제의 결정 문제 버전
Weighted, undirected, complete 그래프 G에서 길이가 K 이하인 Hamiltonian cycle이 존재하는가?
NP-Complete인 optimization problem 존재? => X
[OPT-TSP] : TSP 문제의 최적화 문제 버전
Weighted, undirected, complete 그래프 G에서 가장 짧은 Hamiltonian cycle의 길이는?
NP-Complete에 포함이 안되는 NP-hard
(NP가 아니므로)
OPT-TSP는 NP-Hard 임
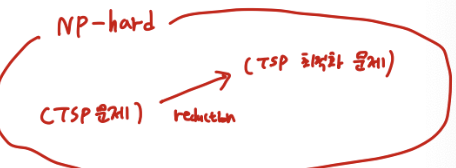
- TSP의 입력을 OPT-TSP에 넣어 최단 경로 길이 x를 계산
- x가 K 이하이면 "Yes" 를, K 보다 크면 "No"를 출력
=> OPT-TSP는 NP-Hard인 TSP 문제를 변환한 것 이므로 NP-Hard 인데 결정문제가 아니므로 NP가 아님
(그러므로 NP-Complete도 될 수 없음)
=> NP-Complete인 Optimization 문제가 존재한다 (X)
다른 NP-Complete 문제의 최적화 버전도 비슷한 방식으로 NP-Hard 임을 증명 가능
'🔥 Algorithm' 카테고리의 다른 글
| L17 - A* Algorithm (3) | 2024.12.07 |
|---|---|
| L16 - NP-Completeness (1) (0) | 2024.12.03 |
| L15 - Boyer-Moore Algorithm (0) | 2024.11.30 |
| L14 - KMP Algorithm (1) | 2024.11.30 |
| L13 - Topological Sorting (0) | 2024.11.29 |
국민대학교에서 "쉽게 배우는 알고리즘" 교재를 이용한
박하명 교수님의 강의 교안을 이용하여 수업 내용을 정리하였습니다
NP-Completeness 개요

P : 다항시간에 풀 수 있는 결정 문제 집합
NP : 비결정론적으로 다항시간에 풀 수 있는 결정 문제 집합
=> 답을 다항시간에 검증할 수 있는 문제
(다항시간에 검증할 수 있으면 NP 문제)
NP-Hard : 모든 NP 문제에서 다항시간 변환되는 문제 집합
=> 검증이 안될 수 도 있음 (NP - Complete와의 차이)
NP-Complete : NP-Hard 이면서 NP인 문제
(결국 NP이기에 yes/no의 결정문제 집합임)
NP-Hard 증명 방법
문제 A가 NP-Hard 임을 증명하는 방법에는 2가지가 있음
1. NP-Hard 정의에 따라 모든 NP문제를 문제 A로 다항시간 변환해봄
=> 이건 사실상 불가능
(모든 NP 문제를 일일이 변화해야함)
2. NP-Hard인 문제 B를 문제 A로 다항시간 변환해봄
=> NP-Hard인 문제 B를 문제 A로 다항시간 변환할 수 있으면 문제 A는 NP-Hard임
문제 A가 NP-Hard임을 증명하고 NP임도 증명
NP-Complete 증명 방법
문제 A가 NP-Hard 임을 증명하고 NP임도 증명하면됨

알려진 NP-Hard 문제에서 다항시간 변환해서 NP-Hard 임을 증명하고
답이 다항시간에 검증되는지 확인하여 NP임도 증명하면됨
NP-Complete 문제들
NP-Complete 문제들은 모두 동일하게 어려움
=> 다항시간 알고리즘이 아직 알려지지 않음
(P = NP가 증명 X)
NP-Complete 문제는 NP-Hard 정의에 따라 서로 변환이 가능함
=> NP-Hard는 모든 NP문제를 다항 시간 내에 풀 수 있음을 의미하는데 결국 모든 NP-Complete 문제는 NP이기에 서로 변환 가능
NP-Complete가 가지는 의미
일단 현재는 P = NP가 증명되지 않았기에 NP 문제를 다항시간에 푸는 알고리즘은 아직 모름
(많은 사람들이 실패함)
만약 P = NP라면 NP-Complete도 P임

만일 NP-Complete 문제 중 단 하나만이라도 다항시간 알고리즘을 발견하면, 모든 NP문제를 다항시간에 풀 수 있음
=> 모든 NP 문제는 NP-Complete 문제로 변환되기 떄문
TSP = NP-Complete?
TSP는 이전에 다뤘었는데 외판원 순환 문제라고해서 모든 정점을 방문하고 시작 정점으로 돌아오는 길이 K이하의 최단 경로가 존재하는가? 에 대한 문제임
TSP가 NP-Complete임을 증명하려면
1. NP-Hard임을 증명
=> HAM-CYCLE을 다항시간 변환
(HAM-CYCLE은 NP-Hard임)
2. NP임을 증명
=> 어떤 순환 경로가 답으로 주어지면
- 이 경로가 모든 노드를 지나는지
- 경로의 합이 K이하인지 다항시간에 확인가능

NP-Complete인 HAM-CYCLE을 변환하여 증명
=> HAM-CYCLE의 입력 G를 TSP의 입력 G'로 변환
- G의 모든 간선의 가중치를 1로 설정
- 없는 간선은 생성하여 가중치를 무한대로 설정
- 정점의 수가 n일 때, O(n^2)의 시간 필요
K=n인 TSP 문제의 정답은 HAM-CYCLE의 정답과 동일하므로
Longest Path = NP-Complete?
LONGEST-PATH는 두 점을 잇는 길이가 K 이상인 단순 경로를 찾는 문제
질문은 s에서 t로 가는 길이가 K 이상인 단순 경로가 존재하는가?
(단순 경로란 같은 정점이 두 번 이상 반복되지 않는 경로)
Longest Path는 NP 인가?
한 경로가 답으로 제시되었을 때 올바른 답인지 검증하는데 다항 시간이 걸림
- s에서 t로 끝나는가? -> O(1)
- 경로가 단순 경로인가? -> O(n)
- 경로의 길이가 K 이상인가? -> O(n)
Longest Path는 NP-Hard 인가?
NP-Complete인 Hamiltonian Path 문제를 다항시간 변환하여 증명
HAM-PATH-2-POINTS는 두 점을 잇는 hamiltonian path를 찾는 문제임
=> s에서 t로 가는 hamiltonian path가 존재하는가?
(hamiltonian path는 그래프의 모든 정점을 한 번씩 지나는 경로임)
HAM-PATH-2-POINTS => LONGEST-PATH

HAM-PATH 의 입력 G를 LONGEST-PATH 입력 G'으로 변환
G의 모든 간선에 weight를 1로 부여하여 G' 생성하고
(변환시간은 O(n^2))
G',s,t를 입력받는 LONGEST-PATH 문제의 답 (K = n - 1 일 때) 이
G,s,t를 입력받는 HAM-PATH-2-POINTS 문제의 답과 동일함
NP-Hardness of Optimization Problems
다항시간 변환의 정의를 확장하여 최적화 문제에 적용

=> 이전에 다뤘던 다항시간 변환의 정의를 확장할 수 있음
- 변환은 다항시간에 이뤄진다.
두 사례의 답이 일치한다.
=> β의 답을 이용하여 α의 답을 구할 수 있다.
[TSP] : TSP 문제의 결정 문제 버전
Weighted, undirected, complete 그래프 G에서 길이가 K 이하인 Hamiltonian cycle이 존재하는가?
NP-Complete인 optimization problem 존재? => X
[OPT-TSP] : TSP 문제의 최적화 문제 버전
Weighted, undirected, complete 그래프 G에서 가장 짧은 Hamiltonian cycle의 길이는?
NP-Complete에 포함이 안되는 NP-hard
(NP가 아니므로)
OPT-TSP는 NP-Hard 임

- TSP의 입력을 OPT-TSP에 넣어 최단 경로 길이 x를 계산
- x가 K 이하이면 "Yes" 를, K 보다 크면 "No"를 출력
=> OPT-TSP는 NP-Hard인 TSP 문제를 변환한 것 이므로 NP-Hard 인데 결정문제가 아니므로 NP가 아님
(그러므로 NP-Complete도 될 수 없음)
=> NP-Complete인 Optimization 문제가 존재한다 (X)
다른 NP-Complete 문제의 최적화 버전도 비슷한 방식으로 NP-Hard 임을 증명 가능
'🔥 Algorithm' 카테고리의 다른 글
| L17 - A* Algorithm (3) | 2024.12.07 |
|---|---|
| L16 - NP-Completeness (1) (0) | 2024.12.03 |
| L15 - Boyer-Moore Algorithm (0) | 2024.11.30 |
| L14 - KMP Algorithm (1) | 2024.11.30 |
| L13 - Topological Sorting (0) | 2024.11.29 |
